Часть четвертая. Вариант 1
Предлагаем Вашему вниманию решение тестовых заданий четвертой части первого варианта ГИА (ДПА) 2012 по математике для одиннадцатого класса.
Четвертая часть аттестационной работы состоит из четырех заданий открытой формы с развернутым ответом. Решение заданий 4.1 — 4.4 должно содержать объяснения. В нем необходимо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. При необходимости решения иллюстрируются схемами, графиками, таблицами.
Задание 4.1
Решить неравенство для каждого значения параметра $$a.$$
$$\sqrt{x^2+8x-9}(x-a)\geqslant 0.$$
Решение:
ОДЗ: $$x^2+8x-9\geqslant 0$$
По теореме Виета $$x_1=-9,\;x_2=1$$ – корни квадратного трехчлена $$x^2+8x-9= 0.$$ Применим формулу разложения квадратного трехчлена на множители и получим $$(x+9)(x-1)\geqslant 0.$$
Для решения неравенства используем метод интервалов.
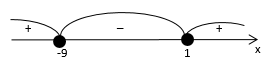
$$x\in(-\infty;-9]\cup [1;\infty).$$
Приступим к решению исходного неравенства.
Так как квадратный корень всегда неотрицательный, т.е. $$\sqrt{x^2+8x-9}\geqslant 0,$$ то получили совокупность:
$$\left[ \begin{matrix} x & = & -9\\ x & = & 1\\ x&-&a & \geqslant & 0 \end{matrix}\right.\Rightarrow \left[\begin{matrix} x & = & -9\\ x & = & 1\\ x & \geqslant & a \end{matrix}\right.$$
Три случая (с учетом ОДЗ):
1) $$a<-9\Rightarrow x\in[a;-9]\cup[1;\infty).$$
2) $$a\in[-9;1]\Rightarrow x\in[1;\infty)\cup\left \{ -9 \right \}.$$
3) $$a>1\Rightarrow x\in[a;\infty)\cup\left \{ -9;1 \right \}.$$
Задание 4.2
Вычислить площадь фигуры, ограниченной графиками функций $$y=|4-x^2|$$ и $$y=4+2|x|.$$
Для нахождения площади фигуры, ограниченной графиками функций, необходимо вычислить определенный интеграл. Но сначала построим графики данных функций.
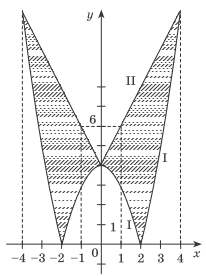
График I функции $$y=|4-x^2|$$ получен путем преобразований (сначала строится парабола $$y=4-x^2,$$ а затем та часть графика, которая ниже оси абсцисс, симметрично отображается относительно этой оси). График II функции $$y=4+2|x|$$ также получен путем преобразований. Данная функция эквивалентна функции $$y=\left\{\begin{matrix} 4+2x,\;x\geqslant 0\\ 4-2x,\;x<0 \end{matrix}\right.$$ (две полупрямые).
Получили фигуру, которая симметрична относительно оси ординат. Вычислим площадь фигуры (воспользуемся свойствами определенного интеграла и формулой Ньютона-Лейбница)
$$S=\int_{-4}^{4}\left ( 4+2|x|-|4-x^2| \right )dx=2\int_{0}^{4}\left ( 4+2|x|-|4-x^2| \right )dx=$$
$$=2\int_{0}^{2}\left ( 4+2x-4+x^2 \right )dx+2\int_{2}^{4}\left ( 4+2x+4-x^2 \right )dx=$$
$$=2\int_{0}^{2}\left ( 2x+x^2 \right )dx+2\int_{2}^{4}\left ( 8+2x-x^2 \right )dx=$$
$$=2\left ( x^2+\frac{x^3}{3} \right )|_{0}^2+2\left ( 8x+x^2-\frac{x^3}{3} \right )|_{2}^{4}=$$
$$=2\left ( 4+\frac{8}{3} \right )+2\left ( 32+16-\frac{64}{3}-16-4+\frac{8}{3} \right )=$$
$$=\frac{40}{3}+\frac{56}{3}=\frac{96}{3}=32$$
Ответ: 32.
Задание 4.3
Углы при основании трапеции равны $$20^{\circ}$$ и $$70^{\circ},$$ а длина отрезка, соединяющего середины оснований, – 2 см. Найти длины оснований трапеции, если длина ее средней линии равна 4 см.
Решение:
Пусть $$ABCD$$ – данная трапеция. $$BP=PC=a,\;AK=KD=b,$$ $$KP=2$$ см – отрезок, соединяющий середины оснований. Продлим боковые стороны трапеции до пересечения в точке $$N.$$ Получили прямоугольный треугольник $$AND$$ (по условию сумма углов при основании равна $$20^{\circ}+70^{\circ}=90^{\circ}$$). $$NK$$ – медиана треугольника $$(AK=KD).$$ Так как основания трапеции параллельны, то $$NK$$ проходит через точку $$P.$$

Длина медианы треугольника, проведенной из вершины прямого угла, равна половине гипотенузы. Следовательно $$NK=AK=KD=b,\; NP=BP=PC=a.$$
$$NK-NP=KP\Rightarrow b-a=2.$$
По условию длина средней линии трапеции равна 4 см, значит
$$\frac{BC+AD}{2}=4\Rightarrow \frac{2a+2b}{2}=4\Rightarrow a+b=2$$
Получили систему двух уравнений с двумя неизвестными
$$\left\{\begin{matrix} b-a=2\;(1)\\ b+a=2\;(2) \end{matrix}\right.$$
$$(1)+(2)\Rightarrow 2b=6\Rightarrow b=3$$
$$(2)+(1)\Rightarrow 2a=2\Rightarrow a=1$$
Получили $$BC=2a=2$$ см, $$AD=2b=6$$ см.
Ответ: 2 см; 6 см.
Задание 4.4
В шар радиуса $$R$$ вписан прямоугольный параллелепипед, диагональ которого образует с плоскостью основания угол $$\alpha,$$ а с меньшей боковой гранью – угол $$\beta.$$ Найти площадь боковой поверхности параллелепипеда.
Решение:

$$ABCDA_1B_1C_1D_1$$ – прямоугольный параллелепипед. $$O$$ – центр описанного шара и середина диагонали $$DB_1.$$ $$\angle B_1DB=\alpha$$ – угол наклона диагонали к плоскости основания. $$\angle B_1DC_1=\beta$$ – угол между диагональю $$DB_1$$ и меньшей гранью ($$DC_1$$ является проекцией диагонали $$DB_1$$ на боковую грань). $$OD=R$$ – радиус шара, значит $$DB_1=2R.$$
Из прямоугольных треугольников по определению тригонометрических функций и теореме Пифагора:
$$\triangle B_1BD:\;BD=2R\cos\alpha,\;BB_1=2R\sin\alpha=CC_1.$$
$$\triangle B_1C_1D:\;C_1D=2R\cos\beta,\;B_1C_1=2R\sin\beta=BC.$$
$$\triangle C_1CD:\;DC^2=C_1D^2-CC_1^2=4R^2(\cos^2\beta-\sin^2\alpha)$$
$$DC=2R\sqrt{\cos^2\beta-\sin^2\alpha}.$$
Найдем площадь боковой поверхности параллелепипеда
$$S=2(BC+DC)\cdot BB_1=2(2R\sin\beta+2R\sqrt{\cos^2\beta-\sin^2\alpha})\cdot2R\sin\alpha=$$
$$=8R^2\sin\alpha(\sin\beta+\sqrt{\cos^2\beta-\sin^2\alpha}).$$
Ответ: $$8R^2\sin\alpha(\sin\beta+\sqrt{\cos^2\beta-\sin^2\alpha}).$$
Источник: Збірник завдань для державної підсумкової атестації з математики: 11 кл. / О.С. Істер, О.І. Глобін, О.В. Комаренко. – К.: Центр навч.-метоод. л-ри, 2012.