Задание 31
Використовуючи графік рівняння $$|y|=1-|x-12|$$ (див. рисунок), знайдіть усі значення параметра $$a$$, при яких система $$\left\{\begin{matrix} |x-12| + |y| = 1 \\ (x-a)^2 + y^2 = 4 \end{matrix}\right.$$ має єдиний розв’язок. У відповідь запишіть їх суму.
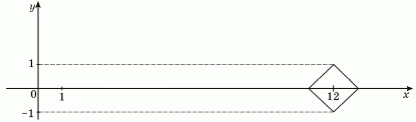
Решение:
$$(x-a)^2 + y^2 = 4$$- уравнение окружности с центром в точке $$(a;0)$$ и радиусом, равным 2.
Решением системы являются точки пересечения графиков функций. Система будет иметь единственное решение лишь в том случае, когда графики пересекаются лишь в одной точке.
Изобразим на рисунке все такие случаи.

Параметр $$a$$ может принимать следующие значения: 9; 11; 13 и 15.
9+11+13+15=48.
Ответ: 48.
Задание 32
Визначте кут між векторами $$\overrightarrow{a}$$ і $$\overrightarrow{b+c}$$ у градусах, якщо відомо, що $$\overrightarrow{a}(2;2)$$, $$\overrightarrow{b}(2;4)$$ і $$\overrightarrow{c}(-2;-6)$$.
Решение:
$$\overrightarrow{b+c}=\overrightarrow{(2+(-2);4+(-6))}=\overrightarrow{(0;-2)}$$
$$\overrightarrow{a}\cdot \overrightarrow{b+c}=2\cdot0+2\cdot(-2)=-4$$
$$|\overrightarrow{a}|=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}, |\overrightarrow{b+c}|=\sqrt{0^2+(-2)^2}=2$$
$$\angle \widehat{(\overrightarrow{a};\overrightarrow{b+c})}=arccos\frac{\overrightarrow{a}\cdot \overrightarrow{b+c}}{|\overrightarrow{a}|\cdot|\overrightarrow{b+c}|}=arccos\frac{-4}{2\sqrt{2}\cdot 2}=arccos (-\frac{1}{2})=$$
$$=\pi-arccos\frac{1}{2}=\pi-\frac{\pi}{4}=\frac{3\pi}{4}=135^{\circ}$$
Ответ: $$135^{\circ}$$
Задание 33
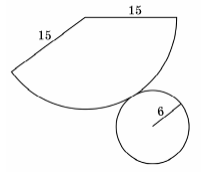
На рисунку зображено розгортку конуса. Визначте відношення площі повної поверхні цього конуса до площі його бічної поверхні.
Решение:
$$S_{1}=\pi R l$$ – площадь боковой поверхности конуса, где $$R$$ – радиус основания, $$l$$ – образующая конуса.
$$S_{2}=\pi R^2$$ – площадь круга.
$$S_{3}=S_{1}+S_{2}$$ – площадь полной поверхности конуса.
$$\frac{S_{3}}{S_{1}}$$ – отношение площади полной поверхности конуса к площади его боковой поверхности.
$$R=6, l=15\Rightarrow S_{1}=6\cdot15\cdot \pi=90\pi, S_{2}=6^2\pi=36\pi,$$
$$S_{3}=90\pi+36\pi=126\pi\Rightarrow \frac{S_{3}}{S_{1}}=\frac{126\pi}{90\pi}=1.4$$
Ответ: 1.4
Задание 34
У правильній трикутній піраміді SABC з основою АВС бічне ребро вдвічі більше за сторону основи. Точки K і L є серединами ребер АС і ВС відповідно. Через пряму KL, паралельно до ребра SС, проведено площину α. Знайдіть кут ϕ між площиною α і площиною (АВС).Решение:
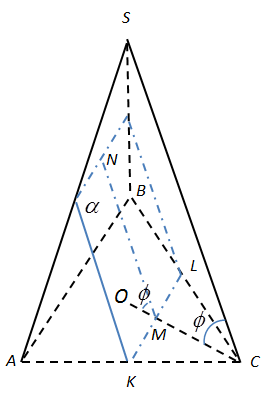
В основании правильный треугольник $$ABC$$, значит $$OC=R=\frac{a\sqrt{3}}{3}$$, где $$O$$ – центр,$$R$$ – радиус описанной около треугольника окружности, $$a$$ – сторона треугольника. По условию ребро в два раза больше стороны основания, т.е. $$SC=2a$$.
$$\angle OMN=\angle OCS=\phi, \angle SOC=90^{\circ}$$ $$\Rightarrow$$ $$\cos\phi=\frac{OC}{SC}=\frac{R}{2a}=\frac{a\sqrt{3}}{2\cdot a\cdot 3}=\frac{1}{2\sqrt{3}}\Rightarrow \phi=arccos\frac{1}{2\sqrt{3}}$$
Ответ: $$\phi=arccos\frac{1}{2\sqrt{3}}$$.
Задание 35
Розв’яжіть систему нерівностей $$\left\{\begin{matrix} \frac{(x+3)(x-2)}{x^2-1} \leqslant 1,\\ 4^{\sqrt{9-x^2}} \leqslant 0.25^{x-3}. \end{matrix}\right.$$Решение:
$$\left\{\begin{matrix} \frac{(x+3)(x-2)}{(x-1)(x+1)} -1 \leqslant 0,\\ 4^{\sqrt{9-x^2}} \leqslant 4^{-x+3}. \end{matrix}\right.$$
$$\left\{\begin{matrix} \frac{(x+3)(x-2)-(x-1)(x+1)}{(x-1)(x+1)} \leqslant 0,\\ \sqrt{9-x^2} \leqslant 3-x. \end{matrix}\right.$$
$$\left\{\begin{matrix} \frac{x^2-2x+3x-6-x^2+1}{(x-1)(x+1)} \leqslant 0,\\ \sqrt{9-x^2} \leqslant 3-x. \end{matrix}\right.$$
$$\left\{\begin{matrix} \frac{x-5}{(x-1)(x+1)} \leqslant 0,\\ \sqrt{9-x^2} \leqslant 3-x. \end{matrix}\right.$$
Рассмотрим первое неравенство системы
$$\frac{x-5}{(x-1)(x+1)}\leqslant 0$$

$$x\in(-\infty;-1)\cup(1; 5]$$
Рассмотрим второе неравенство системы
$$\sqrt{9-x^2} \leqslant 3-x$$
Иррациональное неравенство эквивалентно системе
$$\left\{\begin{matrix} 9-x^2 \geqslant 0\\ 3-x \geqslant 0 \\ (\sqrt{9-x^2})^2 \leqslant (3-x)^2 \end{matrix}\right.$$
$$\left\{\begin{matrix} (x-3)(x+3) \leqslant 0\\ x \leqslant 3 \\ 9-x^2 \leqslant 9+x^2-6x \end{matrix}\right.$$
Для первых двух неравенств системы

$$x\in[-3; 3]$$
Рассмотрим третье неравенство
$$2x^2-6x\geqslant 0$$
$$x(x-3)\geqslant 0$$
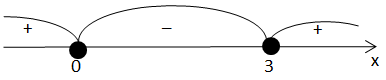
$$x\in(-\infty; 0]\cup[3;\infty)$$
Итак, получили систему
$$\left\{\begin{matrix} x\in(-\infty;-1)\cup(1; 5]\\ x\in[-3; 3]\\ x\in(-\infty; 0]\cup[3;\infty) \end{matrix}\right.$$

$$x\in [-3;-1)\cup \left \{ 3 \right \}$$
Ответ: $$x\in [-3;-1)\cup \left \{ 3 \right \}.$$
Задание 36
Задано функцію $$f(x)=3x^4-4x^3-12x^2$$.- Знайдіть проміжки зростання та спадання функції, екстремуми функції.
- Побудуйте ескіз графіка функції $$f(x)$$.
- Знайдіть кількість коренів рівняння $$f(x)=a$$, де $$a\in \mathbb{R}$$, залежно від значення параметра $$a$$.
Решение:
1. Найдем производную функции $$f(x)=3x^4-4x^3-12x^2$$
$${f}'(x)=12x^3-12x^2-24x$$
Найдем критические точки из условия, когда производная равна нулю либо не существует
$${f}'(x)=0\Rightarrow 12x^3-12x^2-24x=0\Rightarrow 12x(x^2-x-2)=0$$
$$x=0$$ или $$x^2-x-2=0$$
$$x^2-x-2=0$$
По теореме Виета: $$x_{1}\cdot x_{2}=-2, x_{1}+x_{2}=1\Rightarrow x_{1}=-1, x_{2}=2$$
Т.е. $$x=0, x=-1, x=2$$ – критические точки
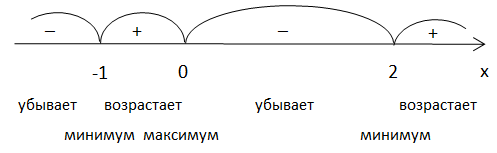
Отметим критические точки на числовой оси, определим знак, который принимает производная на каждом из промежутков. Если на промежутке производная $${f}'(x)>0$$ (ставим знак “+”), то функция $$f(x)$$ возрастает на этом промежутке, а если $${f}'(x)<0$$ (ставим знак “-“), то функция $$f(x)$$ убывает на этом промежутке. Если критическая точка принадлежит области определения функции, то при переходе с “+” на “-” критическая точка является точкой максимума, а с “-” на “+” – минимума. При $$x\in (-\infty; -1)\cup (0;2)$$ функция убывает
При $$x\in (-1;0)\cup (2; \infty)$$ функция возрастает
$$x=-1\Rightarrow y=-5\Rightarrow (-1;-5)$$ – точка минимума
$$x=0\Rightarrow y=0\Rightarrow (0;0)$$ – точка максимума
$$x=2\Rightarrow y=0\Rightarrow (2;-32)$$ – точка минимума
2. Изобразим эскиз графика функции $$f(x)=3x^4-4x^3-12x^2$$
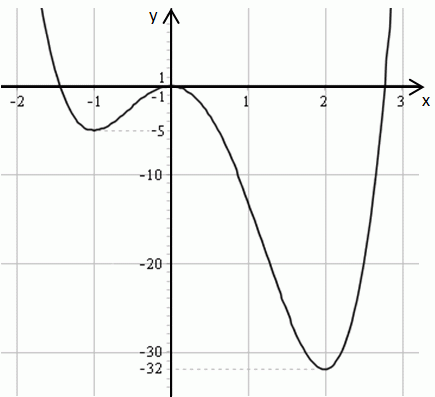
3. Найдем количество корней уравнения $$f(x)=a$$, где $$a\in \mathbb{R}$$, в зависимости от параметра.
Для этого нужно провести прямую $$y=a$$ (параллельно оси Ox). Количество точек пересечения графика функции $$f(x)=3x^4-4x^3-12x^2$$ с прямой $$y=a$$ является количеством корней уравнения $$f(x)=a$$.
1) $$a\in(-\infty;-32)$$ – нет корней;
2) $$a=-32$$ – 1 корень;
3) $$a\in(-32;-5)\cup (0;\infty)$$ – 2 корня;
4) $$a=0$$ – 3 корня;
5) $$a\in (-5;0)$$ – 4 корня.