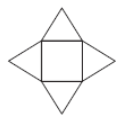
На рисунке изображена развертка пирамиды, состоящая из квадрата со стороной 10 см, и четырех правильных треугольников. Определить площадь боковой поверхности этой пирамиды в (см2).
А. $$100\sqrt{3}$$
Б. 100
В. $$400\sqrt{3}$$
Г. $$100\cdot(1+\sqrt{3})$$
Д. 200
Решение
Площадь боковой поверхности будет состоять из площадей четырех правильных треугольников со стороной 10 см (в основании пирамиды квадрат со стороной 10 см). Остается вспомнить формулу площади правильного треугольника:
$$S_{\triangle}=\frac{\sqrt{3}}{4}a^2$$
Значит площадь боковой поверхности пирамиды равна
$$S=4\cdot S_{\triangle}=4\cdot\frac{\sqrt{3}}{4}a^2=\sqrt{3}a^2=10^2\sqrt{3}=100\sqrt{3}$$
Ответ: А.