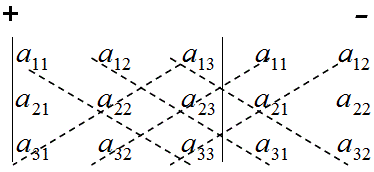Елементи теорії визначників і матриць

Основні означення

Запис $$A_{(n\times m)}$$ слід читати, як матриця $$A$$ розмірності $$(n\times m)$$, де $$n$$ – кількість рядків, а $$m$$ – стовпців.

Матрицею називається таблиця чисел $$A=\begin{pmatrix} a_{11} &\cdots &a_{1m} \\ \vdots & & \\ a_{n1}& \cdots & a_{nm} \end{pmatrix}$$.

Визначником називається число, записане певним чином:

$$detA=|A|=\Delta A=\begin{vmatrix} a_{11} &\cdots &a_{1n} \\ \vdots & & \\ a_{n1}& \cdots & a_{nn} \end{vmatrix}.$$

Доречно підкреслити, що первісним поняттям для понять «визначник» і «матриця» є поняття квадратної матриці. Отже, визначник розглядається як похідний від матриці або відповідний до неї. Визначник завжди має квадратну форму і має певне значення, тоді як матриця може мати не тільки квадратну, але і прямокутну форму, а також набувати форми стовпця і рядка. Матриця не обчислюється, а тому не має певного значення.

Розглянемо квадратні матриці, визначники другого, третього та більш високого порядку, основні властивості визначників.

Другий порядок

Нехай маємо числа $$a_{11}, a_{12}, a_{21}, a_{22}$$. Таблиця, яка має вигляд $$\begin{pmatrix} a_{11} & a_{12}\\ a_{21}& a_{22} \end{pmatrix},$$ зветься квадратною матрицею другого порядку, числа $$a_{11}, a_{12}, a_{21}, a_{22}$$ – її елементами, причому перший індекс у записі числа вказує на номер рядка, в якому стоїть цей елемент, а другий – на номер стовпця.

Визначником другого порядку називається число, яке вираховується таким чином:

$$\Delta =\begin{vmatrix} a_{11} & a_{12}\\ a_{21}& a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}$$.

Приклади:

$$\begin{vmatrix} 3 & -2\\ 4 & 6 \end{vmatrix}=3\cdot6-(-2)\cdot4=26$$

$$\begin{vmatrix} \sqrt{a} & -1\\ a & \sqrt{a} \end{vmatrix}=\sqrt{a}\cdot\sqrt{a}-(-1)\cdot a=2a$$

Третій та більш високий порядок. Основні властивості

Цілком аналогічно, розглядаючи таблицю виду $$\begin{pmatrix} a_{11} & a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32} & a_{33} \end{pmatrix}$$, де $$a_{i,k}, (i=\overline{1,3}, k=\overline{1,3})$$ – деякі числа, назвати її матрицею третього порядку.

Визначником третього порядку називається число, яке вираховується таким чином:

$$\Delta =\begin{vmatrix} a_{11} & a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32} & a_{33} \end{vmatrix}=\begin{matrix} a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32}-\\ -a_{13}\cdot a_{22}\cdot a_{31}-a_{11}\cdot a_{23}\cdot a_{32}-a_{12}\cdot a_{21}\cdot a_{33}. \end{matrix}$$

Для знаходження цього числа можна застосувати один із трьох способів.
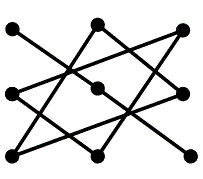
Перший – спосіб трикутників або Саррюса – передбачає використання двох схем, в яких елементи визначника зображені точками.

За схемою 1 обчислюється вираз, що є сумою трьох добутків із трьох різних елементів, коли добутки беруться зі своїми знаками.

Схема 1 – Обчислення виразу: $$a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32}$$

За схемою 2 обчислюється вираз, що є сумою трьох добутків із трьох різних елементів, коли добутки беруть з протилежними знаками.

Схема 2 – Обчислення виразу: $$-a_{13}\cdot a_{22}\cdot a_{31}-a_{11}\cdot a_{23}\cdot a_{32}-a_{12}\cdot a_{21}\cdot a_{33}$$

Визначник дорівнює алгебраїчній сумі цих двох виразів, тобто, $$\Delta =\begin{matrix} a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32}-\\ -a_{13}\cdot a_{22}\cdot a_{31}-a_{11}\cdot a_{23}\cdot a_{32}-a_{12}\cdot a_{21}\cdot a_{33}. \end{matrix}$$

Другий спосіб обчислення визначника третього порядку передбачає дописування перших двох стовпців визначника з правої його сторони і такі обчислення: добутки елементів на головній діагоналі і паралелях до неї (вони беруться зі своїми знаками), добутки побічної діагоналі і паралелях до неї (беруться з протилежними знаками)

Третій спосіб полягає у використанні теореми розкладу – визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчні доповнення.

Наводимо пояснення: мінором $$M_{ik}$$ елемента $$a_{ik}$$ називається визначник, який утворюють незакреслені елементи визначника, якщо в ньому здійснити закреслення елементів $$i$$-того рядка і $$k$$-того стовпця. Алгебраїчним доповненням $$A_{ik}$$ називається добуток мінора на вираз $$(-1)^{i+k}$$, отже, $$A_{ik}=(-1)^{i+k}M_{ik}$$.

Наведемо основні властивості визначників:

1. Величина визначника не зміниться, якщо рядки та стовпці його поміняти місцями.
2. Якщо у визначнику поміняти місцями лише два рядки або стовпці, то знак зміниться на протилежний.
3. Якщо всі елементи деякого рядка (стовпця) помножити на будь-яке число, то величина визначника також помножиться на те саме число. Звідси зрозуміло, що спільний множник всіх елементів рядка (стовпця) можна виносити за знак визначника.
4. Якщо визначник містить два пропорційних рядки (стовпці), то величина його дорівнює нулю. Отже, якщо елементи деякого рядка (стовпця) дорівнюють нулю, то і сам визначник дорівнює нулю.
5. Величина визначника не змінюється, якщо до елементів одного рядка (стовпця) додати елементи другого рядка (стовпця), помножені на одне й теж число.
6. Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчні доповнення (теорема розкладу).
7. Сума добутків елементів будь-якого рядка (стовпця) на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) дорівнює нулю.

Приклад: Обчислити визначник третього порядку за допомогою 3 способів.

Знайдемо визначник за правилом Саррюса:

$$\begin{vmatrix} 2 & 1 & 1\\ 5 & 1 & 3\\ 2&1&2 \end{vmatrix}=2\cdot1\cdot2+1\cdot3\cdot2+1\cdot5\cdot1-1\cdot1\cdot2-1\cdot5\cdot2-2\cdot3\cdot1=-3$$

Знайдемо визначник, дописав справа перші два стовпця

$$\begin{vmatrix} 2 & 1 & 1\\ 5 & 1 & 3\\ 2&1&2 \end{vmatrix}\begin{matrix} 2 & 1\\ 5 & 1\\ 2 & 1 \end{matrix}=2\cdot1\cdot2+1\cdot3\cdot2+1\cdot5\cdot1-1\cdot1\cdot2-2\cdot3\cdot1-1\cdot5\cdot2=-3$$

Спочатку виконаємо деякі перетворення: від другого та третього рядка віднімемо перший рядок (властивість 5), а потім здійснимо розклад визначника за елементами другого стовпця (властивість 6).

$$\begin{vmatrix} 2 & 1 & 1\\ 5 & 1 & 3\\ 2&1&2 \end{vmatrix}=\begin{vmatrix} 2 & 1 & 1\\ 3 & 0 & 2\\ 0&0&1 \end{vmatrix}=1\cdot(-1)^{1+2}\cdot \begin{vmatrix}3&2\\0&1\end{vmatrix}=-3$$

Визначники більш високого порядку (більше 3) знаходяться за допомогою теореми розкладу (див. приклад).

Сума матриць

Сумою двох матриць $$A$$ і $$B$$ однакової розмірності називається матриця $$C$$, елементи якої дорівнюють сумі відповідних елементів матриць $$A$$ і $$B$$.
Операція додавання матриць має властивості:

1. $$A+B=B+A$$
2. $$\left (A+B \right )+C=A+(B+C)$$
3. $$A+H=A$$, де $$H$$- нульова матриця (всі елементи є нулями).

Приклад:

$$\begin{pmatrix} 2 & 5 & 7\\ 1 & -6 & 4 \end{pmatrix}+\begin{pmatrix} -5 & 5 & 12\\ 1 & 4 & 3 \end{pmatrix}=\begin{pmatrix} 2+(-5) & 5+5 & 7+12\\ 1+1 & -6+4 & 4+3 \end{pmatrix}=\begin{pmatrix} -3 & 10 & 19\\ 2 & -2 & 7 \end{pmatrix}$$

Добуток матриць

Добутком матриці $$A_{(n\times k)}$$ на матрицю $$B_{(k\times m)}$$ називається матриця $$C_{(n\times m)}$$, кожний елемент якої дорівнює сумі добутків елементів $$i$$-го рядка матриці $$A$$ на відповідні елементи $$j$$-го стовпця матриці $$B$$.

Властивості добутку матриць

1. $$A\cdot B\neq B\cdot A$$
2. $$\left (A\cdot B \right )\cdot C=A\cdot \left (B\cdot C \right )$$
3. $$A\cdot E=E\cdot A=A$$, де $$E$$ – одинична матриця (на головній діагоналі стоять одиниці, інші елементи – нулі)

Приклади:

$$\begin{pmatrix} 1 & 3 & 5\\ 4 & 2 & -1 \end{pmatrix}\cdot\begin{pmatrix} 0 & 3\\ 2 & 4\\ 7&-1 \end{pmatrix}=\begin{pmatrix} 1\cdot0+3\cdot2+5\cdot7 & 1\cdot3+3\cdot4+5\cdot(-1)\\ 4\cdot0+2\cdot2+(-1)\cdot7 & 4\cdot3+2\cdot4+(-1)\cdot(-1) \end{pmatrix}=$$

$$=\begin{pmatrix} 41 & 10\\ -3 & 21 \end{pmatrix}$$

$$\begin{pmatrix} 0 & 2\\ 1 & 0 \end{pmatrix}\cdot \begin{pmatrix} 1\\ 3 \end{pmatrix}=\begin{pmatrix} 0+6\\ 1+0 \end{pmatrix}=\begin{pmatrix} 6\\ 1 \end{pmatrix}$$

$$\begin{pmatrix} 1 &2&3 \end{pmatrix}\cdot \begin{pmatrix} 1\\3\\-5\\8 \end{pmatrix}$$ неможливо знайти добуток (кількість стовпців першої матриці не збігається з кількістю рядків другої матриці)

Обернена матриця

Оберненою матрицею $$A^{-1}$$ для матриці $$A$$ називають матрицю, для якої виконується рівність $$A\cdot A^{-1}=A^{-1}\cdot A=E$$ і яка має вигляд:
$$A^{-1}=\frac{1}{|A|}\begin{pmatrix} A_{11} & A_{21} & A_{31}\\ A_{12} & A_{22}& A_{32}\\ A_{13}& A_{23}& A_{33} \end{pmatrix}$$, де $$|A|$$ – визначник матриці $$A, A_{ij}$$ – алгебраїчні доповнення.
Для того, щоб знайти обернену матрицю, потрібно:

1. Обчислити визначник матриці $$A$$. Якщо $$|A|=0$$, то оберненої матриці не існує. Якщо ні, то виконувати наступні дії.
2. Знайти алгебраїчні доповнення до всіх елементів матриці $$A$$.
3. Записати обернену матрицю за формулою, що наведена вище. Слід звернути увагу на те, що матриця складена з алгебраїчних доповнень та транспонована (рядки записані замість стовпців, а стовпці замість рядків).
4. Зробити перевірку $$A\cdot A^{-1}=A^{-1}\cdot A=E$$.

Приклад:

$$A=\begin{pmatrix} 2 & 1 & 1\\ 5 & 1 & 3\\ 2&1&2 \end{pmatrix}$$

$$|A|=-3$$ (дивись приклади обчислення визначників третього порядку)

$$A_{11}=(-1)^{1+1}\begin{vmatrix} 1 & 3\\ 1 & 2 \end{vmatrix}=-1$$ ,

$$A_{21}=(-1)^{2+1}\begin{vmatrix} 1 & 1\\ 1 & 2 \end{vmatrix}=-1$$,

$$A_{31}=(-1)^{3+1}\begin{vmatrix} 1 & 1\\ 1 & 3 \end{vmatrix}=2$$,

$$A_{12}=(-1)^{1+2}\begin{vmatrix} 5 & 3\\ 2 & 2 \end{vmatrix}=-4$$,

$$A_{22}=(-1)^{2+2}\begin{vmatrix} 2 & 1\\ 2 & 2 \end{vmatrix}=2$$,

$$A_{32}=(-1)^{3+2}\begin{vmatrix} 2 & 1\\ 5 & 3 \end{vmatrix}=-1$$,

$$A_{13}=(-1)^{1+3}\begin{vmatrix} 5 & 1\\ 2 & 1 \end{vmatrix}=3$$,

$$A_{23}=(-1)^{2+3}\begin{vmatrix} 2 & 1\\ 2 & 1 \end{vmatrix}=0$$,

$$A_{33}=(-1)^{3+3}\begin{vmatrix} 2 & 1\\ 5 & 1 \end{vmatrix}=-3$$.

$$A^{-1}=-\frac{1}{3}\begin{pmatrix} -1 &-1 &2 \\ -4& 2 &-1 \\ 3& 0 &-3 \end{pmatrix}=\begin{pmatrix} \frac{1}{3} &\frac{1}{3} &-\frac{2}{3} \\ \frac{4}{3}& -\frac{2}{3} &\frac{1}{3} \\ -1& 0 &1 \end{pmatrix}$$

$$A^{-1}\cdot A=-\frac{1}{3}\begin{pmatrix} -1 &-1 &2 \\ -4& 2 &-1 \\ 3& 0 &-3 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1\\ 5 & 1 & 3\\ 2&1&2 \end{pmatrix}=$$

$$=-\frac{1}{3}\begin{pmatrix} -2-5+4 & -1-1+2 &-1-3+2 \\ -8+10-2 & -4+2-1 & -4+6-2\\ 6+0-6 & 3+0-3& 3+0-6 \end{pmatrix}=\begin{pmatrix} 1 & 0 &0 \\ 0& 1& 0\\ 0 & 0 & 1 \end{pmatrix}=E$$

Якщо знайти добуток $$A\cdot A^{-1}$$, то також вийде одинична матриця.

Продолжение: Вычисление определителей третьего и четвертого порядка; Сумма, произведение, транспонирование матриц; Решение СЛУ.