Для острых углов в декартовой системе координат
Пусть дана декартова система координат. Из начала координат провели отрезок $$OM$$ под углом $$\alpha$$ к оси $$Ox:$$
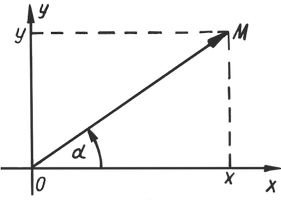
Синусом называется отношение:
$$\sin\alpha=\frac{y}{|OM|}$$
Косинусом называется отношение:
$$\cos\alpha=\frac{x}{|OM|}$$
Тангенсом называется отношение:
$$\text{tg}\alpha=\frac{y}{x}\;\left ( \alpha\neq\frac{\pi}{2}+k\pi,\; k\in\mathbb{Z} \right )$$
Котангенсом называется отношение:
$$\text{ctg}\alpha=\frac{x}{y}\;\left ( \alpha\neq k\pi,\; k\in\mathbb{Z} \right )$$
Посредством единичной окружности
Рассмотрим единичную окружность:

$$\sin\alpha=y$$
$$\cos\alpha=x$$
$$\text{tg}\alpha$$ – ордината точки $$Q$$
$$\text{ctg}\alpha$$ – абсцисса точки $$K$$
Знаки тригонометрических функций по четвертям
