Деревня расположена на берегу реки, а школа – на шоссе, пересекающем реку под прямым углом. Зимой школьник ходит из деревни в школу напрямик на лыжах и тратит на дорогу 40 мин. Весной, в распутницу, он идет берегом реки до шоссе, а дальше – по шоссе до школы, и тратит на дорогу 1 ч 10 мин. Наконец, осенью он проходит вдоль реки половину расстояния, отделяющего деревню от шоссе, а дальше идет напрямик. При этом он доходит до школы быстрее, чем за 57 мин. Установите, что дальше: деревня от шоссе или школа от реки, если известно, что пешком школьник ходит всегда с одной и той же скоростью, а на лыжах со скоростью на 25% большей (реку и шоссе считать прямыми линиями).
Решение
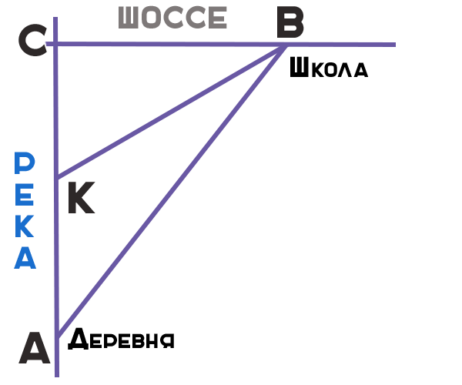
Введем обозначения.
$$A$$ – место расположения деревни, $$B$$ – место расположения школы, $$C$$ – точка пересечения реки и шоссе.
$$\triangle ABC$$: $$\angle C=90^{\circ}$$, $$AB=c$$, $$AC=b$$, $$BC=a$$. Точка $$K$$ – середина расстояния от деревни до шоссе вдоль реки, $$AK=KC=\frac{b}{2}$$, $$BK=\sqrt{a^2+(\frac{b}{2})^2}$$ – расстояние от половины пути по реке до школы (по теореме Пифагора из прямоугольного треугольника $$\triangle KCB$$).
Примем за единицу скорость пешего передвижения школьника, тогда скорость на лыжах равна $$1.25$$
Найдем время, за которое может добраться школьник из деревни в школу напрямик, если будет идти пешком: $$1.25\cdot 40=50$$ минут.
ЗИМА: расстояние $$c$$ за 40 минут на лыжах или 50 минут пешком.
ВЕСНА: расстояние $$a+b$$ за 70 минут пешком.
ОСЕНЬ: расстояние $$\frac{b}{2}+\sqrt{a^2+(\frac{b}{2})^2}$$ менее, чем за 57 минут пешком.
Итак, $$a+b=70$$, тогда $$b=70-a$$
Из треугольника $$\triangle ABC$$ по теореме Пифагора $$a^2+b^2=c^2$$
$$a^2+(70-a)^2=50^2$$
$$a^2+70^2+a^2-140a-50^2=0$$
$$2a^2-140a+(70-50)(70+50)=0$$
$$2a^2-140a+2400=0$$
$$a^2-70a+1200=0$$
По теореме Виета: $$a_1=30$$, $$a_2=40$$
Тогда $$b_1=40$$, $$b_2=30$$
Проверим осеннее неравенство $$\frac{b}{2}+\sqrt{a^2+(\frac{b}{2})^2} < 57$$
- $$a=30$$, $$b=40$$
$$\frac{40}{2}+\sqrt{30^2+(\frac{40}{2})^2} < 57$$
$$\sqrt{900+400} < 37$$
$$\sqrt{1300} < \sqrt{1369}$$ – верно - $$a=40$$, $$b=30$$
$$\frac{30}{2}+\sqrt{40^2+(\frac{30}{2})^2} < 57$$
$$\sqrt{1600+225} < 42$$
$$\sqrt{1825} < \sqrt{1764}$$ – ложно
Значит расстояние от деревни до шоссе равно 40, что больше расстояния от школы до реки, равного 30.
Ответ: деревня дальше от шоссе, чем школа от реки.