Через точки $$A$$ и $$B$$, лежащих на окружностях верхнего и нижнего оснований цилиндра и не принадлежащих одной образующей, проведена плоскость параллельно оси цилиндра. Расстояние от центра нижнего основания до этой плоскости равно $$\sqrt{10}$$ см, а площадь полученного сечения – $$54\sqrt{10}$$ см2. Определить длину отрезка $$AB$$ (в см), если площадь боковой поверхности цилиндра равна $$180\pi$$ см2.
Решение
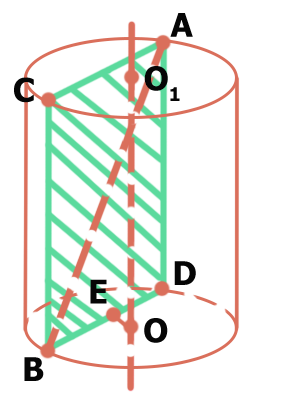
Рассмотрим рисунок. $$A$$ принадлежит нижнему основанию цилиндра, $$B$$ – верхнему. Прямоугольник $$ADBC$$ – сечение цилиндра плоскостью, параллельной к оси цилиндра $$OO_{1}$$. $$OE=\sqrt{10}$$ см – расстояние от центра нижнего основания до плоскости сечения. Площадь сечения $$S_{ADBC}=54\sqrt{10}$$ см2. Площадь боковой поверхности цилиндра $$S_{\text{бок. цил.}}=180\pi$$ см2. $$AB$$ – диагональ прямоугольника $$ADBC$$.
Площадь боковой поверхности цилиндра можно найти по формуле $$S_{\text{бок. цил.}}= 2\pi R H$$, где $$R$$ – радиус основания цилиндра, $$H$$ – высота цилиндра. Значит $$2\pi R H=180\pi$$ или $$RH=90$$.
Получили $$H=\frac{90}{R}$$.
Так как площадь сечения является площадью прямоугольника, то $$S_{ADBC}=AD\cdot BD$$, где $$AD=H$$ является и высотой цилиндра. Т.е. $$H\cdot BD=54\sqrt{10}$$.
Подставим $$H$$, выразим $$BD$$ и получим $$BD=\frac{54\sqrt{10}\cdot R}{90}$$.
Или $$BD=\frac{3\sqrt{10}}{5}R$$.
Рассмотрим треугольник $$\triangle BEO$$: $$\angle E=90^{\circ}$$, $$OE=\sqrt{10}$$, $$BE=\frac{1}{2}BD$$, $$OB=R$$ – радиус основания цилиндра. По теореме Пифагора $$OB^2=OE^2+BE^2$$ или $$R^2=10+\frac{1}{4}BD^2$$.
Подставим $$BD$$ и получим $$R^2=10+\frac{1}{4}\cdot (\frac{3\sqrt{10}}{5}R)^2$$.
$$R^2=10+ \frac{90}{100}R^2$$
$$0.1R^2=10$$
$$R^2=100$$
$$R=10$$ см
Тогда $$BD=6\sqrt{10}$$ см и $$H=9$$ см.
Рассмотрим прямоугольный треугольник $$\triangle ADB$$. По теореме Пифагора $$AB^2=AD^2+BD^2$$.
$$AB=\sqrt{9^2+(6\sqrt{10})^2}=\sqrt{81+360}=\sqrt{441}=21$$ см.
Ответ: 21