Часть третья. Вариант 2
Предлагаем Вашему вниманию решение тестовых заданий третьей части второго варианта ГИА (ДПА) по математике для девятого класса за 2012 год.
Третья часть аттестационной работы состоит из трех заданий открытой формы с развернутым ответом. Решение заданий 3.1 — 3.3 должно содержать объяснения. В нем необходимо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. При необходимости решения иллюстрируются схемами, графиками, таблицами.
Задание 3.1
З міста А в місто В виїхав велосипедист. Через 3 год у тому самому напрямі з міста А виїхав мотоцикліст і прибув у місто В одночасно з велосипедистом. Знайдіть швидкість велосипедиста, якщо вона менша за швидкість мотоцикліста на 45 км/год, а відстань між містами дорівнює 60 км.
Решение:
Пусть скорость мотоциклиста $$x$$ км/ч, тогда скорость велосипедиста $$x-45$$ км/ч. Расстояние между городами равно 60 км, тогда время в пути, которое затратили мотоциклист и велосипедист, равно соответственно $$\frac{60}{x}$$ ч и $$\frac{60}{x-45}$$ ч.
Учитывая тот факт, что велосипедист был в пути на 3 часа дольше, чем мотоциклист, составим и решим уравнение:
$$\frac{60}{x-45}-\frac{60}{x}=3,\;x\neq45,\;x\neq0$$
$$\frac{60x-60x+2700-3x^2+135x}{x(x-45)}=0$$
$$x^2-45x-900=0$$
По теореме Виета:
$$x_1=-15$$ (посторонний корень), $$x_2=60$$.
Итак, скорость мотоциклиста 60 км/ч, значит скорость велосипедиста 60-45=15 км/ч.
Ответ: 15 км/ч.
Задание 3.2
Побудуйте графік функції $$y=\frac{x^2+6x+8}{x+2}-\frac{2x-x^2}{x}.$$
Решение:
Данная функция не определена при $$x=-2,\;x=0$$.
Упростим ее, воспользовавшись теоремой Виета, формулой разложения квадратного трехчлена на множители и вынесением общего множителя за скобки:
$$y=\frac{(x+4)(x+2)}{x+2}-\frac{x(2-x)}{x}=x+4-(2-x)=2x+2$$
Получили:
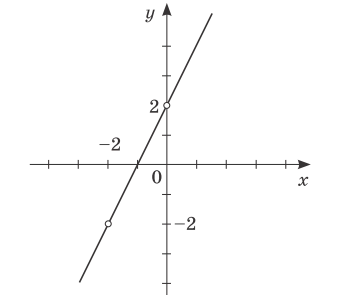
$$y=2x+2,\;x\neq-2,\;x\neq0$$
Изобразим график данной функции:
Задание 3.3
Знайдіть площу трапеції, основи якої дорівнюють 10 см і 14 см, а бічні сторони – 13 см і 15 см.
Решение:
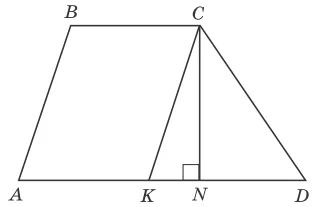
$$ABCD$$ – трапеция, $$AB=13,\;BC=10,\;CD=15,\;AD=14,\;CN$$ – высота трапеции.
Площадь трапеции вычисляется по формуле: $$S_{ABCD}=\frac{BC+AD}{2}\cdot CN.$$
Проведем $$CK\parallel AB$$. Получили $$ABCK$$ – параллелограмм, у которого
$$CK=AB=13,\;AK=BC=10$$.
Рассмотрим треугольник $$CKD:$$
$$CK=13,\;CD=15,\;KD=AD-AK=14-10=4$$, $$CN$$ – высота треугольника.
С одной стороны площадь треугольника равна
$$S=\frac{1}{2}KD\cdot CN\Rightarrow CN=\frac{2S}{KD}$$.
С другой стороны по формуле Герона площадь равна
$$S=\sqrt{p(p-a)(p-b)(p-c)},\; p=\frac{a+b+c}{2}$$.
$$p=\frac{13+15+4}{2}=16\Rightarrow S=\sqrt{16(16-13)(16-15)(16-4)}=\sqrt{16\cdot3\cdot1\cdot12}=$$
$$=\sqrt{4^2\cdot3^2\cdot2^2}=4\cdot3\cdot2=24$$
Тогда $$CN=\frac{2\cdot24}{4}=12$$
$$S_{ABCD}=\frac{10+14}{2}\cdot12=12^2=144$$
Ответ: 144 см2.