Предлагаем Вашему вниманию решение 1 варианта государственной итоговой аттестации (ГИА) или на украинском державної підсумкової атестації (ДПА) по математике для 9 класса за 2012 год.
Аттестационная работа состоит из четырех частей. Эти части отличаются формой тестовых заданий и уровнем сложности.
Ученики общеобразовательных классов выполняют все задания первой, второй и третьей частей аттестационной работы.
Ученики классов с углубленным изучением математики выполняют задания всех четырех частей аттестационной работы.
Государственная итоговая аттестация (ГИА) по математике проводится на протяжении 3 академических часов для учеников общеобразовательных классов и 4 академических часов для учеников классов с углубленным изучением математики.
Часть первая
В каждом из 12 заданий первой части по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ.
Отметьте правильные, на Ваш взгляд, ответы и нажмите Завершить тест. После этого нажмите кнопку Показать вопросы, чтобы ознакомиться с решением для тех заданий, где Вы допустили ошибку. Желаем удачи в прохождении теста.
Часть вторая
Вторая часть аттестационной работы состоит из четырех заданий открытой формы с коротким ответом.
Задания 2.1 — 2.4
2.1 Обчисліть $$3\sqrt{1\frac{4}{9}}\cdot\sqrt{1\frac{3}{13}}-\sqrt{(-4)^6}.$$
Решение:
Воспользуемся свойствами корней и степеней
$$3\sqrt{1\frac{4}{9}}\cdot\sqrt{1\frac{3}{13}}-\sqrt{(-4)^6}=3\sqrt{\frac{13}{9}\cdot\frac{16}{13}}-\sqrt{4^6}=\frac{3\sqrt{16}}{\sqrt{9}}-4^3=4-4^3=$$
$$=4(1-16)=-60$$
Ответ: $$-60.$$
2.2 Графіком квадратичної функції є парабола, що має вершину у початку координат і проходить через точку А(2; -8). Задайте цю функцію формулою.
Решение:
Так как парабола проходит через начало координат, то ее уравнение может быть задано в виде $$y=ax^2$$
Подставим в уравнение координаты точки А
$$-8=a\cdot2^2\Rightarrow a=-2$$
Получили уравнение искомой функции: $$y=-2x^2$$
Ответ: $$y=-2x^2$$
2.3 Розв’яжіть систему рівнянь
$$\left\{\begin{matrix} x^2-2xy+y^2=9\\ 2x-y= 5\end{matrix}\right.$$
Решение:
Левую часть первого уравнения свернем по формуле квадрат разности
Во втором уравнении выразим $$y$$
$$\left\{\begin{matrix} (x-y)^2 = 9\\ y = 2x- 5 \end{matrix}\right.$$
Подставим $$y$$ из второго уравнения в первое
$$(x-2x+5)^2=9$$
$$(5-x)^2=9$$
$$25+x^2-10x=9$$
$$x^2-10x+16=0$$
По теореме Виета получим
$$x_1=2,\;x_2=8$$
1) $$x_1=2\Rightarrow y_1=-1$$
2) $$x_2=8\Rightarrow y_2=11$$
Ответ: $$x_1=2,\;y_1=-1;\;x_2=8,\;y_2=11.$$
2.4 Зовнішній кут правильного многокутника становить $$\frac{1}{5}$$ внутрішнього. Знайдіть кількість сторін цього многокутника.
Решение:
Пусть $$\alpha$$ – внутренний угол, а $$\beta$$ – внешний. $$\beta=\pi-\alpha$$
По условию $$\beta=\frac{1}{5}\alpha$$
$$\frac{1}{5}\alpha=\pi-\alpha\Rightarrow \alpha=\frac{5\pi}{6}$$
Сумма внутренних углов правильного многоугольника равна $$n\cdot\alpha$$, где $$n$$ – количество сторон. Сумма внутренних углов плоского выпуклого $$n$$-угольника равна $$(n-2)\pi.$$
$$(n-2)\pi=n\cdot\frac{5\pi}{6}$$
$$n-2=\frac{5}{6}n$$
$$\frac{1}{6}n=2$$
$$n=12$$
Ответ: 12
Часть третья
Третья часть аттестационной работы состоит из трех заданий открытой формы с развернутым ответом. Решение заданий 3.1 – 3.3 должно содержать объяснения. В нем необходимо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. При необходимости решения иллюстрируются схемами, графиками, таблицами.
Задания 3.1 — 3.3
3.1 Автомобіль мав проїхати 1200 км із певною запланованою швидкістю. Після того, як він проїхав третину шляху із цією швидкістю, автомобіль витратив на зупинку 2 год. Збільшивши швидкість на 20 км/год, автомобіль прибув у пункт призначення вчасно. Якою була швидкість автомобіля до зупинки?
Решение:
$$S=1200$$ км
По условию задачи автомобиль проехал треть пути, сделал остановку на 2 часа и продолжил путь с увеличенной скоростью.
$$S_1=\frac{S}{3}=400,\;S_2=S-S_1=800,\;v_1=v,\;v_2=v+20,\;v>0$$
Найдем время, за которое автомобиль проехал первую и вторую часть пути
$$S_1=v_1\cdot t_1\Rightarrow 400=v\cdot t_1\Rightarrow t_1=\frac{400}{v}$$
$$S_2=v_2\cdot t_2\Rightarrow 800=(v+20)\cdot t_2\Rightarrow t_2=\frac{800}{v+20}$$
Найдем общее время
$$t=t_1+2+t_2=\frac{400}{v}+2+\frac{800}{v+20}$$
Подставим общее время в формулу для нахождения расстояния
$$S=v\cdot t$$
$$v\cdot\left ( \frac{400}{v}+2+\frac{800}{v+20} \right )=1200$$
Упростим полученное уравнение
$$400+2v+\frac{800v}{v+20}=1200$$
$$2v+\frac{800v}{v+20}=800$$
$$v+\frac{400v}{v+20}=400$$
$$v\cdot(v+20)+400v=400(v+20)$$
$$v^2+20v+400v=400v+8000$$
Получили квадратное уравнение относительно первоначальной скорости
$$v^2+20v-8000=0$$
Найдем корни по теореме Виета:
$$v=-100$$ (посторонний корень) и $$v=80$$
Ответ: 80 км/час
3.2 Доведіть, що значення виразу
$$\left ( \frac{3-a}{a^2-2a+1} -\frac{2}{1-a}\right )\left ( \frac{a^2-3a}{a^3+3a^2+3a+1} +\frac{1}{a^2+2a+1}\right )$$
є додатним при всіх допустимих значеннях змінної.
Доказательство:
Упростим первоначальное выражение.
Воспользуемся формулами сокращенного умножения: квадрат разности, куб суммы и квадрат суммы
$$\left ( \frac{3-a}{(a-1)^2} -\frac{2}{1-a}\right )\left ( \frac{a^2-3a}{(a+1)^3} +\frac{1}{(a+1)^2}\right )=$$
Приведем дроби к общему знаменателю
$$=\frac{3-a+2(a-1)}{(a-1)^2}\cdot \frac{a^2-3a+a+1}{(a+1)^3}=$$
$$a \not= \pm1$$
Раскроем скобки и приведем подобные слагаемые
$$=\frac{a+1}{(a-1)^2}\cdot \frac{a^2-2a+1}{(a+1)^3}=$$
Опять воспользуемся формулой квадрат разности и после этого сократим дроби
$$=\frac{a+1}{(a-1)^2}\cdot \frac{(a-1)^2}{(a+1)^3}=\frac{1}{(a+1)^2}$$
Получили $$\frac{1}{(a+1)^2}>0,\;a \not= \pm1$$
ч.т.д.
3.3 Бісектриса гострого кута паралелограма ділить його сторону у відношенні 3:4, рахуючи від вершин тупого кута. Периметр паралелограма дорівнює 80 см. Знайдіть довжини його сторін.
Решение:

$$\frac{BE}{EC}=\frac{3}{4}\Rightarrow BE=3x,\;EC=4x,\;x$$ – коэффициент пропорциональности.
Тогда $$BC=3x+4x=7x.$$
$$\angle BAE=\angle EAD$$ так как $$AE$$ – биссектриса, $$\angle BEA=\angle EAD$$ как внутренние накрест лежащие при параллельных прямых $$AD,$$ $$BC$$ и секущей $$AE.$$ Значит треугольник $$ABE$$ является равнобедренным, то есть $$AB=BE=3x.$$
Найдем сумму двух сторон из периметра параллелограмма
$$P=2(AB+BC)=80\Rightarrow AB+BC=40$$
Получили $$AB+BC=3x+7x=10x\Rightarrow 10x=40\Rightarrow x=4$$
$$AB=12,\;BC=28$$
Ответ: 12 см; 28 см; 12 см; 28 см.
Часть четвертая
Четвертая часть аттестационной работы состоит из двух заданий открытой формы с развернутым ответом. Решение заданий 4.1 – 4.2 должно содержать объяснения. В нем необходимо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. При необходимости решения иллюстрируются схемами, графиками, таблицами.
Задания 4.1 — 4.2
4.1 При яких значеннях параметра $$a$$ рівняння $$\left |x^2-4|x|+3 \right |=a$$ має шість розв’язків?
Решение:
Рассмотрим две функции $$y=\left |x^2-4|x|+3 \right |$$ и $$y=a.$$ Пересечение графиков данных функций в шести точках и будет решением задания.
Построим график первой функции $$y=\left |x^2-4|x|+3 \right |.$$
Для этого сначала построим график функции $$y=x^2-4x+3$$ при $$x\geqslant 0.$$ Это парабола $$y=(x-2)^2-1$$ с вершиной в точке $$(2;-1),$$ ветви которой направлены вверх.
Так как функция $$y=x^2-4|x|+3$$ является четной функцией, то отобразим график функции $$y=x^2-4x+3$$ при $$x\geqslant 0$$ относительно оси $$Oy$$ (оси ординат).
Для построения графика функции $$y=\left |x^2-4|x|+3 \right |$$ необходимо отобразить относительно оси $$Ox$$ ту часть графика функции $$y=x^2-4|x|+3,$$ которая ниже оси абсцисс.
$$y=a$$ – прямая, параллельная оси абсцисс.
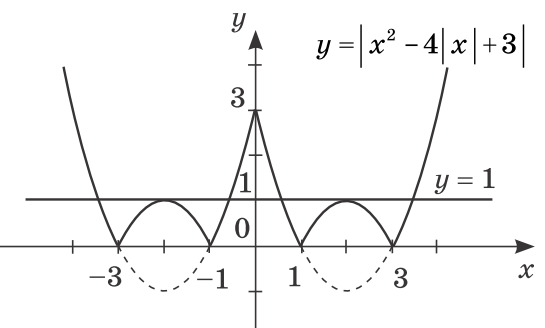
При $$a=1$$ уравнение $$\left |x^2-4|x|+3 \right |=a$$ имеет шесть решений.
Ответ: $$a=1.$$
4.2 Знайдіть площу трикутника, якщо дві його сторони дорівнюють 1 см і $$\sqrt{15}$$ см, а медіана, яка проведена до третьої сторони, дорівнює 2 см.
Решение:
Введем обозначения: $$a,\;b,\;c$$ – стороны треугольника, $$m_c$$ – медиана к стороне $$c.$$ Тогда $$a=1,\;b=\sqrt{15},\;m_c=2.$$
Вспомним соотношение в произвольном треугольнике для медианы
$$m_c=\frac{\sqrt{2a^2+2b^2-c^2}}{2}$$
Найдем $$c$$
$$4m_c^2=2a^2+2b^2-c^2\Rightarrow c^2=2a^2+2b^2-4m_c^2$$
$$c=\sqrt{2a^2+2b^2-4m_c^2}=\sqrt{2\cdot1+2\cdot15-4\cdot4}=\sqrt{16}=4$$
Получили соотношение $$c^2=a^2+b^2,$$ то есть треугольник прямоугольный ($$\angle C=90^{\circ}$$).
Вспомним формулу площади для прямоугольного треугольника
$$S=\frac{1}{2}ab$$
Подставим значения сторон и найдем площадь
$$S=\frac{\sqrt{15}}{2}$$
Ответ: $$\frac{\sqrt{15}}{2}$$ см2