Часть третья. Вариант 1
Предлагаем Вашему вниманию решение тестовых заданий третьей части первого варианта ГИА (ДПА) 2012 по математике для одиннадцатого класса.
Третья часть аттестационной работы состоит из трех заданий открытой формы с развернутым ответом. Решение заданий 3.1 — 3.3 должно содержать объяснения. В нем необходимо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. При необходимости решения иллюстрируются схемами, графиками, таблицами.
Задание 3.1
Вычислить значение выражения $$\log_2\left ( \log_3 \cos\frac{\pi}{6}-\log_3 \sin\frac{\pi}{6}\right )$$.
Решение:
Воспользуемся свойствами логарифмов, определением и таблицей значений некоторых углов тригонометрических функций.
$$\log_2\log_3\textup{ctg}\,\frac{\pi}{6}=\log_2\log_3\sqrt{3}=\log_2\frac{1}{2}=-1$$
Ответ: $$-1$$.
Задание 3.2
Найти координаты точки на прямой $$y=2-7x$$, если разность квадратов абсциссы и ординаты этой точки является наибольшей.
Решение:
Пусть $$A(x;y)$$ – искомая точка. Рассмотрим функцию разности квадратов абсциссы и ординаты этой точки $$f(x;y)=x^2-y^2$$.
По условию $$y=2-7x$$. Подставим в функцию $$f(x;y)$$ и получим функцию, зависящую только от одной переменной $$x$$.
$$f(x)=x^2-(2-7x)^2$$
Преобразуем полученную функцию, используя формулу квадрат разности и приведение подобных слагаемых
$$f(x)=x^2-(4+49x^2-28x)=x^2-4-49x^2+28x=-48x^2+28x-4$$
Так как по условию разность квадратов абсциссы и ординаты точки $$A(x;y)$$ должна быть наибольшей, то найдем наибольшее значение функции $$f(x)$$. Для этого найдем производную данной функции.
$${f}'(x)=-96x+28$$
Найдем значения переменной, в которых производная равна нулю $${f}'(x)=0$$.
$$-96x+28=0\Rightarrow x=\frac{7}{24}$$.
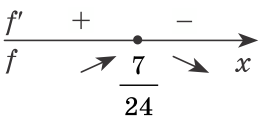
При $$x=\frac{7}{24}$$ функция $$f(x)$$ принимает наибольшее значение. Подставим его в уравнение прямой: $$y\left (\frac{7}{24} \right )=2-\frac{49}{24}=\frac{48-49}{24}=-\frac{1}{24}$$.
$$A\left (\frac{7}{24};-\frac{1}{24} \right )$$ – искомая точка.
Ответ: $$A\left (\frac{7}{24};-\frac{1}{24} \right )$$.
Задание 3.3
Высота конуса равна диаметру его основания. Найти отношение площади его основания к площади боковой поверхности.
Решение:
Рассмотрим осевое сечение конуса. Получили равнобедренный треугольник $$ASB$$. По условию высота конуса $$SO$$ (она же высота треугольника $$ASB$$) равна диаметру основания конуса $$AB$$.
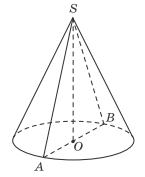
Рассмотрим прямоугольный треугольник из треугольника $$SOA:\;\angle SOA=90^{\circ}.$$ Пусть $$AB=SO=x$$, тогда $$AO=\frac{x}{2}$$. По теореме Пифагора найдем гипотенузу $$AS$$, которая является боковой стороной в треугольнике $$ASB$$.
$$AS=\sqrt{x^2+\frac{x^2}{4}}=\sqrt{\frac{5x^2}{4}}=\frac{x\sqrt{5}}{2}$$.
Площадь основания конуса вычисляется как площадь круга
$$S_1=\pi R^2=\pi AO^2=\frac{x^2\pi}{4}$$.
Площадь боковой поверхности конуса вычисляется по формуле
$$S_2=\pi\cdot R\cdot l=\pi \cdot AO\cdot AS=\pi\cdot\frac{x}{2}\cdot\frac{x\sqrt{5}}{2}=\frac{\pi x^2\sqrt{5}}{4}$$.
Найдем отношение площади основания конуса к площади его боковой поверхности
$$\frac{S_1}{S_2}=\frac{\frac{\pi x^2}{4}}{\frac{\pi x^2\sqrt{5}}{4}}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$$.
Ответ: $$\frac{\sqrt{5}}{5}$$.
Источник: Збірник завдань для державної підсумкової атестації з математики: 11 кл. / О.С. Істер, О.І. Глобін, О.В. Комаренко. – К.: Центр навч.-метоод. л-ри, 2012.