Задание №21
До кожного виразу при $$a>0$$ доберіть тотожно йому рівний.
| 1 | $$\frac{2a^5}{a^6}$$ | А | $$2a^{-1}$$ |
| 2 | $$(2a)^5\cdot a^6$$ | Б | $$2a^{\frac{6}{5}}$$ |
| 3 | $$(2a^6)^5$$ | В | $$2a^{\frac{5}{6}}$$ |
| 4 | $$\sqrt[6]{64a^5}$$ | Г | $$32a^{30}$$ |
| Д | $$32a^{11}$$ |
Решение:
Задание на упрощение выражения. Воспользуемся свойствами корней и степеней, получим:
$$\frac{2a^5}{a^6}=2a^{5-6}=2a^{-1}$$
$$(2a)^5\cdot a^6=2^5a^5a^6=32a^{5+6}=32a^{11}$$
$$(2a^6)^5=2^5a^{5\cdot 6}=32a^{30}$$
$$\sqrt[6]{64a^5}=(2^6a^5)^{\frac{1}{6}}=(2^6)^{\frac{1}{6}}(a^5)^{\frac{1}{6}}=2a^{\frac{5}{6}}$$
Ответ: 1-А; 2-Д; 3-Г; 4-В.
Задание №22
Кожній точці поставте у відповідність функцію, графіку якої належить ця точка.
| 1 | $$K(0;1)$$ | А | $$y=2x+2$$ |
| 2 | $$N(-1;0)$$ | Б | $$y=\text{ctg}x$$ |
| 3 | $$O(0;0)$$ | В | $$y=\text{tg}x$$ |
| 4 | $$M(0;-1)$$ | Г | $$y=\sqrt{x}-1$$ |
| Д | $$y=2^x$$ |
Решение:
Проверяется подстановкой координат точек в функцию.
$$O(0;0)\in y=\text{tgx}$$
$$M(0;-1)\in y=\sqrt{x}-1$$
$$N(-1;0)\in y=2x+2$$
$$K(0;1)\in y=2^x$$
Ответ: 1-Д; 2-А; 3-В; 4-Г.
Задание №23
Розв’яжіть рівняння. Установіть відповідність між кожним рівнянням та кількістю його коренів на відрізку $$[-5;5]$$
| 1 | $$x^4+5x^2+4=0$$ | А | жодного |
| 2 | $$\frac{x^3-4x}{x^3+8}=0$$ | Б | один |
| 3 | $$\log _{3}x=-2$$ | В | два |
| 4 | $$\cos ^2 x-\sin^2x=1$$ | Г | три |
| Д | чотири |
Решение:
1) $$\cos ^2 x-\sin^2x=1\Rightarrow \cos2x=1\Rightarrow 2x=2\Pi n,n \in \mathbb{Z}\Rightarrow$$
$$x=\Pi n,n \in \mathbb{Z}, \Pi\approx 3.14$$
$$x=-\Pi;0;\Pi$$ – корни, которые принадлежат отрезку $$[-5;5]$$
3 корня
2) $$\log _{3}x=-2\Rightarrow \log _{3}x=\log _{3}3^{-2}\Rightarrow x=\frac{1}{9}$$
1 корень
3) $$\frac{x^3-4x}{x^3+8}=0\Rightarrow \frac{x^2(x-2)(x+2)}{(x+2)(x^2-2x+4)}=0$$
$$x=0, x=2, x\neq -2, x^2-2x+4\neq 0,$$ т.к. $$D_{1}=1-4<0$$
2 корня
4) $$x^4+5x^2+4=0\Rightarrow x^2=t\geqslant 0, t^2+5t+4=0$$
По теореме Виета: $$t_{1}=-1<0, t_{2}=-4<0$$ – не удовлетворяют условию $$t\geq 0$$
корней нет
Ответ: 1-А; 2-В; 3-Б; 4-Г.
Задание №24
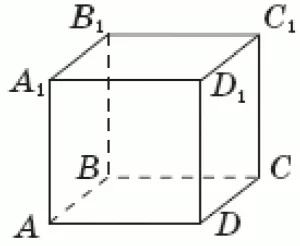
На рисунку зображено куб $$ABCDA_{1}B_{1}C_{1}D_{1}$$. До кожного початку речення доберіть його закінчення так, щоб утворилося правильне твердження.
| 1 | Пряма $$A_{1}B$$ | А | паралельна площині $$AA_{1}B_{1}B$$ |
| 2 | Пряма $$AC$$ | Б | $$AA_{1}B_{1}B$$ перпендикулярна площині |
| 3 | Пряма $$CD_1$$ | В | належить площині $$AA_{1}B_{1}B$$ |
| 4 | Пряма $$CB$$ | Г | має з площиною $$AA_{1}B_{1}B$$ лише дві спільні точки |
| Д | утворює з площиною $$AA_{1}B_{1}B$$ кут $$45^{\circ}$$ |
Решение:
Пряма $$CB$$ перпендикулярна площині $$AA_{1}B_{1}B$$
Пряма $$CD_1$$ паралельна площині $$AA_{1}B_{1}B$$
Пряма $$AC$$ утворює з площиною $$AA_{1}B_{1}B$$ кут $$45^{\circ}$$
Пряма $$A_{1}B$$ належить площині $$AA_{1}B_{1}B$$
Задание №25
Батьки разом із двома дітьми: Марійкою (4 роки) та Богданом (7 років) – збираються провести вихідний день у парку атракціонів. Батьки дозволяють кожній дитині відвідати не більше троьх атракціонів і кожний атракціон – лише по одному разу. Відомо, що на атракціони “Електричні машинки” і “Веселі гірки” допускають лише дітей старше 6 років. На “Паравозик” Богдан не піде. Для відвідування будь-якого атракціону необхідно купити квиток для кожної дитини. Скористувавшись таблицею, визначте максимальну суму коштів (у грн), що витратять батьки на придбання квитків для дітей.
| Назва атракціону | Вартість 1 квитка для 1 дитини, грн |
| Веселі гірки | 17 |
| Паравозик | 16 |
| Електричні машинки | 20 |
| Карусель | 12 |
| Батут | 15 |
| Дитяча рибалка | 8 |
| Лебеді | 13 |
Решение:
Т.к. Богдан не пойдет на “Паравозик”, то по максимально возможной цене для него остаются билеты на следующие аттракционы: “Электрические машинки” (20 грн), “Веселые горки” (17 грн) и “Батут” (15 грн). Итого 20+17+15=52 грн.
Т.к. Марийке 4 года, то она не может пойти на аттракционы “Электрические машинки” и “Веселые горки”, значит по максимально возможной цене для нее остаются билеты на следующие аттракционы: “Паравозик” (16 грн), “Батут” (15 грн) и “Лебеди” (13 грн). Итого 16+15+13=4 4грн.
Получаем: 52+44=96 грн – максимальная сумма, которую потратят родители на приобретение билетов.
Ответ: 96 грн.
Задание №26
Скільки існує різних дробів $$\frac{a}{b},$$ якщо $$a$$ набуває значень 1; 2 або 4, а $$b$$ набуває значень 5; 7; 11; 13 або 17?
Решение:
Задача на “Правило умножения”.
Согласно правилу умножения, если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Естественным образом обобщается на произвольную длину последовательности.
$$a$$ и $$b$$ можно выбрать 3-мя и 5-ю способами соответственно, значит по правилу умножения существует 15 разных дробей вида $$\frac{a}{b}.$$
Ответ: 15.
Задание №27
Розв’яжіть систему рівнянь $$\left\{\begin{matrix} y-x=9\\ \frac{x+8}{2y-5}=2 \end{matrix}\right.$$. Запишіть у відповідь добуток $$x_{0}\cdot y_{0},$$ якщо пара $$(x_{0}; y_{0})$$ є розв’язком цієї системи рівнянь.
Решение:
Из первого уравнения выразим $$y=x+9$$ и подставим его во второе уравнение системы.
$$\frac{x+8}{2(x+9)-5}=2\Rightarrow \frac{x+8}{2x+18-5}=2\Rightarrow \frac{x+8}{2x+13}=2\Rightarrow$$
$$\frac{x+8}{2x+13}-\frac{2(2x+13)}{2x+13}=0\Rightarrow \frac{x+8-4x-26}{2x+13}=0\Rightarrow$$
$$\frac{-3x-18}{2x+13}=0\Rightarrow -3x-18=0, 2x+13\neq 0\Rightarrow$$
$$x=-6, x\neq -\frac{13}{2}\Rightarrow y=-6+9\Rightarrow y=3$$
$$x_{0}=-6, y_{0}=3\Rightarrow x_{0}\cdot y_{0}=-18$$
Ответ: -18.
Задание №28
Обчисліть значення виразу $$\log_{a}500-\log_{a}4$$, якщо $$\log_{5}a=\frac{1}{4}.$$
Решение:
$$\log_{a}500=\log_{a}{5^3\cdot 4}=\log_{a}5^3+\log_{a}4=3\log_{a}5+\log_{a}4$$
Подставим в первоначальное выражение
$$\log_{a}500-\log_{a}4=3\log_{a}5-\log_{a}4+\log_{a}4=3\log_{a}5=\frac{3}{\log_{5}a}$$
Но по условию $$\log_{5}a=\frac{1}{4}$$, значит $$\frac{3}{\log_{5}a}=3:\frac{1}{4}=12$$
Ответ: 12.
Задание №29
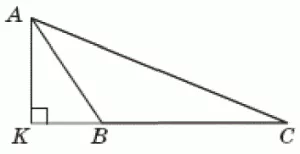
У трикутнику $$\triangle ABC$$ основа висоти $$AK$$ лежить на продовженні сторони $$BC$$ (див. рисунок). $$AK=6,KB=2\sqrt{3}$$. Радіус описаного навколо трикутника $$\triangle ABC$$ кола дорівнює $$15\sqrt{3}.$$ Визначте довжину $$AC$$.
Решение:
Из прямоугольного треугольника $$\triangle AKB$$ по теореме Пифагора найдем $$AB.$$
$$AB^2=AK^2+BK^2\Rightarrow AB=\sqrt{AK^2+BK^2}=$$
$$=\sqrt{6^2+(2\sqrt{3})^2}=\sqrt{16\cdot3}=4\sqrt{3}$$
Воспользуемся формулой для вычисления высоты в произвольном треугольнике:
$$h_{a}=\frac{bc}{2R}$$, где $$h_a$$ – высота, опущенная на сторону $$a,$$ $$R$$ – радиус окружности, описаной около треугольника. $$b$$ и $$c$$ – две другие стороны треугольника.
Т.о. $$AK=\frac{AB\cdot AC}{2R}\Rightarrow AC=\frac{AK\cdot 2R}{AB}=\frac{6\cdot 2\cdot 15 \sqrt{3}}{4\sqrt{3}}=45$$
Ответ: 45.
Задание №30
Обчисліть $$\frac{1}{\pi}\int_{-5}^{0}\sqrt{25-x^2}dx,$$ використовуючи рівняння кола $$x^2+y^2=25,$$ зображеного на рисунку.
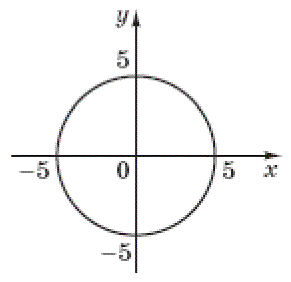
Решение:
Определенный интеграл $$\int_{-5}^{0}\sqrt{25-x^2}dx$$ – площадь четверти круга (см. рисунок)
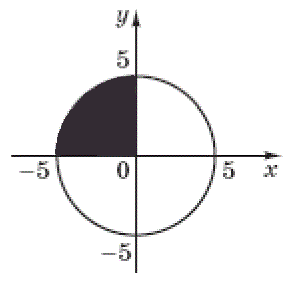
Площадь круга вычисляется по формуле: $$S=\pi R^2$$
Значит $$\int_{-5}^{0}\sqrt{25-x^2}dx=\frac{\pi R^2}{4}=\frac{\pi 5^2}{4}=6.25\pi$$
Отсюда $$\frac{1}{\pi}\int_{-5}^{0}\sqrt{25-x^2}dx=6.25$$
Ответ: 6.25.
Задание №31
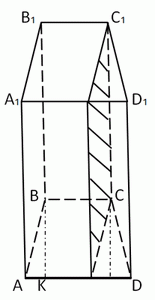
Основою прямої призми $$ABCDA_{1}B_{1}C_{1}D_{1}$$ є рівнобічна трапеція $$ABCD$$. Основа $$AD$$ трапеції дорівнює висоті трапеції і в шість разів більша за основу $$BC$$. Через бічне ребро $$CC_1$$ призми проведено площину паралельно ребру $$AB.$$ Знайдіть площу утвореного перерізу (у см2), якщо об’єм призми дорівнює 672 см3, а її висота – 8 см.
Решение:
Объем призмы можно вычислить по формуле: $$V=SH$$, где $$S$$ – площадь основания, $$H$$ – высота призмы. Площадь трапеции можно вычислить по формуле: $$S=\frac{BC+AD}{2}\cdot h,$$ где $$BC, AD$$ – основания трапеции, $$h$$ – высота трапеции.
По условию $$h=AD=6BC.$$ Подставим в формулу вычисления площади трапеции, а затем вычислим $$BC:$$
$$S=\frac{BC+6BC}{2}\cdot 6BC=21BC^2\Rightarrow V=21BC^2\cdot H\Rightarrow BC=\sqrt{\frac{V}{21H}}$$
$$\Rightarrow BC=\sqrt{\frac{V}{21H}}=\sqrt{\frac{672}{21\cdot 8}}=\sqrt{4}=2$$
Значит $$h=AD=6\cdot 2=12.$$
Трапеция равнобедренная, т.е. $$AB=DC$$. Если опустить высоты из точек $$B$$ и $$C$$ на $$AD,$$ то получится прямоугольник, а слева и справа от него два равных прямоугольных треугольника. Рассмотрим один из них.
$$\triangle ABK: \angle K=90^{\circ}, BK=h=12, AK=\frac{AD-BC}{2}=\frac{12-2}{2}=5.$$
По теореме Пифагора найдем гипотенузу
$$AB=\sqrt{AK^2+BK^2}=\sqrt{5^2+12^2}=\sqrt{25+144}=\sqrt{169}=13.$$
Сечение призмы – прямоугольник со сторонами, равными стороне $$AB$$ и высоте $$H.$$
Площадь этого сечения равна: $$S_{1}=AB\cdot H=13\cdot 8=104.$$
Ответ: 104.
Задание №32
При якому найменшому цілому значенні параметра $$a$$ рівняння
$$\sqrt{2x+15}\cdot (\sqrt{x^2+18x+81}-\sqrt{x^2-10x+25})=a\sqrt{2x+15}$$
має лише два різні корені?
Решение:
ОДЗ: $$2x+15\geqslant 0\Rightarrow x\geqslant -7.5$$
$$\sqrt{2x+15}\cdot (\sqrt{(x+9)^2}-\sqrt{(x-5)^2})-a\sqrt{2x+15}=0$$
$$\sqrt{2x+15}\cdot (|x+9|-|x-5|-a)=0$$
$$\sqrt{2x+15}=0$$ или $$|x+9|-|x-5|-a=0$$
$$x= -7.5$$ или $$|x+9|-|x-5|-a=0$$
Модули обнуляются соответственно при $$x= -9$$ и $$x= 5$$
С учетом этого и ОДЗ, получаем 2 промежутка: $$x \in [-7.5;5)$$ и $$x \in [5;+\infty)$$
I. $$x \in [-7.5;5).$$ Раскроем модули: $$x+9+x-5-a=0\Rightarrow x=\frac{a-4}{2}$$
из ОДЗ и условия лишь 2 разных корней: $$\frac{a-4}{2}> -7.5\Rightarrow a>-11\Rightarrow a=-10$$
II. $$x \in [5;+\infty)$$
$$x+9-x+5-a=0\Rightarrow a=14 (\forall x\in \mathbb{R})$$
Получили бесконечное множество решений, что не удовлетворяет условию.
Ответ: -10.