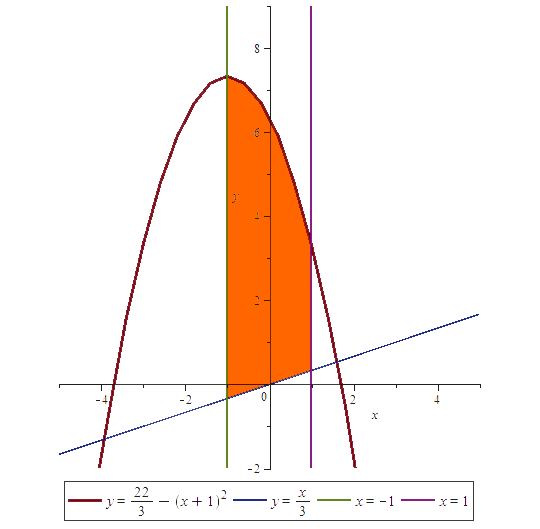
Вычислить площадь фигуры, ограниченной графиком функции $$y=\frac{22}{3}-(x+1)^2$$ и прямыми $$y=\frac{x}{3}, x=-1$$ и $$x=1.$$
Решение
Для нахождения площади такой фигуры (см. рисунок) необходимо вычислить интеграл $$\int\limits_{-1}^{1}(\frac{22}{3}-(x+1)^2-\frac{x}{3})dx=$$
Повторите материалы по теме Интегрирование
$$=\frac{22}{3}\int\limits_{-1}^{1}dx-\int\limits_{-1}^{1}(x+1)^2d(x+1)-\frac{1}{3}\int\limits_{-1}^{1}xdx=$$
$$=[\frac{22}{3}x-\frac{(x+1)^3}{3}-\frac{x^2}{2}]|_{-1}^{1}=$$
$$=(\frac{22}{3}-\frac{8}{3}-\frac{1}{2})-(-\frac{22}{3}-0-\frac{1}{2})=\frac{22+22-8}{3}=\frac{36}{3}=12$$
Ответ: 12.