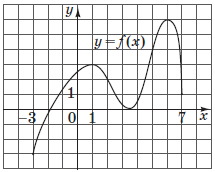
На рисунке изображен график непрерывной функции $$y=f(x),$$ определенной на отрезке $$[-3;7].$$ Сколько всего точек экстремума у этой функции на отрезке $$[-3;7]?$$
А. 1
А. 2
В. 3
Г. 5
Д. 6
Решение:
Функция $$y=f(x)$$ имеет максимум в точке $$x_0,$$ если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку $$x_0.$$ Другими словами если существует окрестность точки $$x_0$$ такая, что для всех $$x\neq x_0$$ из этой окрестности имеет место неравенство $$f(x) < f(x_0).$$
Функция $$y=f(x)$$ имеет минимум в точке $$x_0,$$ если существует окрестность точки $$x_0$$ такая, что для всех $$x\neq x_0$$ из этой окрестности имеет место неравенство $$f(x) > f(x_0).$$
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Очевидно, что таких точек экстремума на отрезке $$[-3;7]$$ для непрерывной функции $$y=f(x)$$ три: два максимума $$x_1=1; x_3=6$$ и один минимум $$x_2=3.5.$$
Ответ: В.