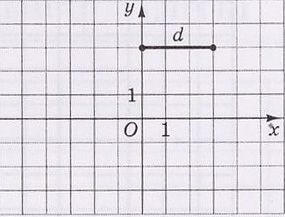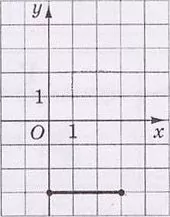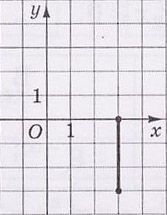Тест состоит из 34 заданий разных форм и длится 150 минут.
Задания оцениваются следующим образом:
За выполнение тестового задания с выбором одного правильного ответа (№ 1-20) можно получить максимум 1 тестовый балл (за правильный ответ). За выполнение тестового задания на установление соответствия (логические пары) (№ 21-24) можно получить максимум 4 тестовых балла (по 1 баллу за каждую верную логическую пару). Задания 25-34 – задания открытой формы с коротким ответом. Тестовые задания 25, 26 являются структурными, состоят из двух частей и оцениваются максимум 2 баллами (по 1 баллу за правильный ответ). За выполнение тестового задания открытой формы с коротким ответом (№ 27-34) можно получить максимум 2 тестовых балла (2 балла за верный ответ). Максимальное количество тестовых баллов, которые можно набрать, выполнив все задания теста по математике, – 56.
Навигация (только номера заданий)
0 из 34 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
Информация
Желаем удачи в прохождении теста
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 34
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
Рубрики
- Нет рубрики 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- С ответом
- С отметкой о просмотре
- Задание 1 из 34
1.
Укажите запись числа 0.351 в стандартном виде.
- Задание 2 из 34
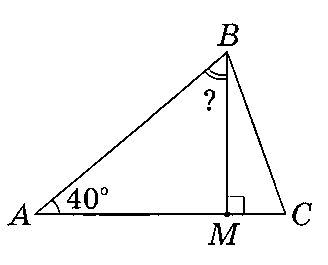
2.
В треугольнике $$ABC$$ проведена высота $$BM$$ (см. рисунок). Определить градусную меру угла $$MBA,$$ если $$\angle A=40^{\circ}.$$
- Задание 3 из 34
3.
Решить уравнение $$\frac{x}{2}+\frac{x}{3}=2.$$
- Задание 4 из 34
4.
Какая из приведенных последовательностей является геометрической прогрессией со знаменателем $$q < 0? $$
- Задание 5 из 34
5.
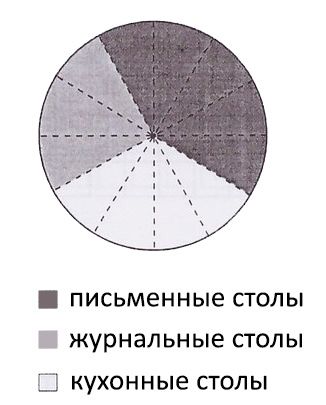
На круговой диаграмме (круг разделен пунктирными линиями на равные секторы) показано распределение количества столов, проданных магазином в течении месяца (см. рисунок). Общее количество проданных столов за этот период составило 108. Сколько было среди них журнальных столов?

- Задание 6 из 34
6.
Если число $$b$$ составляет $$47\%$$ от положительного числа $$a,$$ то $$b=$$
- Задание 7 из 34
7.
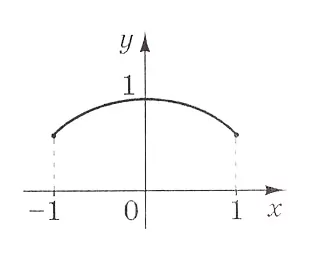
На рисунке изображен фрагмент графика одной из приведенных функций на отрезке $$[-1; 1].$$ Укажите эту функцию.

- Задание 8 из 34
8.
Укажите промежуток, которому принадлежит корень уравнения $$3^x\cdot4^x=\frac{1}{144}.$$
- Задание 9 из 34
9.
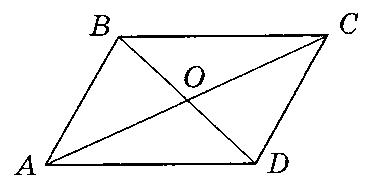
На рисунке изображен параллелограмм $$ABCD,$$ диагонали которого пересекаются в точке $$O.$$ Укажите пару коллинеарных векторов.

- Задание 10 из 34
10.
Окружность задана уравнением $$x^2+y^2=9.$$ Определить координаты точки, принадлежащей кругу, ограниченному этой окружностью.
- Задание 11 из 34
11.
Укажите правильное неравенство, если $$a=\sin 120^{\circ}, b=\cos 120^{\circ}.$$
- Задание 12 из 34
12.
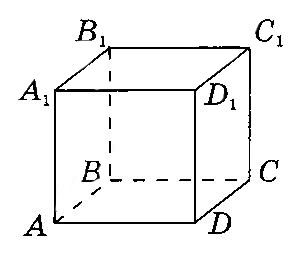
На рисунке изображен куб $$ABCDA_1B_1C_1D_1,$$ ребро которого равно 1 см. Вычислить расстояние от точки $$A$$ до прямой $$B_1C_1.$$

- Задание 13 из 34
13.
Найти все значения $$x,$$ при которых значение выражения $$2-5x$$ принадлежит промежутку $$(-3;6).$$
- Задание 14 из 34
14.
Функция $$y=f(x)$$ возрастает на промежутке $$(-\infty;\infty).$$ Какое из приведенных чисел может быть значением данной функции в точке $$x=8,$$ если $$f(1)=-2, f(9)=5?$$
- Задание 15 из 34
15.
Длина окружности основания цилиндра равна $$18\pi$$ см. Определить площадь боковой поверхности этого цилиндра, если его высота равна 7 см.
- Задание 16 из 34
16.
$$|2-\sqrt{5}|+|2+\sqrt{5}|=$$
- Задание 17 из 34
17.
Точка $$M$$ не принадлежит плоскости $$\alpha.$$ Какие из приведенных утверждений являются правильными?
I. Через точку $$M$$ можно провести лишь одну плоскость, параллельную плоскости $$\alpha.$$
II. Через точку $$M$$ можно провести лишь одну плоскость, перпендикулярную к плоскости $$\alpha.$$
III. Через точку $$M$$ можно провести лишь одну плоскость, пересекающую $$\alpha$$ под углом $$45^{\circ}.$$
- Задание 18 из 34
18.
Найти производную функции $$y=x^7\ln x.$$
- Задание 19 из 34
19.
Объем конуса равен 64 см3. Через середину высоты этого конуса параллельно его основанию проведена плоскость. Полученное сечение является основанием меньшего конуса, вершина которого совпадает с вершиной заданного. Найти объем меньшего конуса.
- Задание 20 из 34
20.
Решить неравенство $$3 + \log_{2}x\geqslant0.$$
- Задание 21 из 34
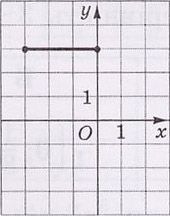
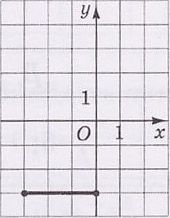
21.
На рисунке изображен отрезок $$d$$ на координатной плоскости $$xy.$$ Установите соответствие между отрезком и рисунком, на котором он изображен.

Элементы сортировки
- отрезок, симметричный отрезку $$d$$ относительно оси $$x$$
- отрезок, симметричный отрезку $$d$$ относительно оси $$y$$
- отрезок, симметричный отрезку $$d$$ относительно точки $$O$$
- отрезок, в который переходит отрезок $$d$$ вследствие поворота вокруг точки $$O$$ на угол $$90^{\circ}$$ против движения часовой стрелки
-
- Задание 22 из 34
22.
Установите соответствие между заданным выражением и выражением, тождественно равным ему, если $$a\neq 0; a\neq 1; a\neq -1.$$
Элементы сортировки
- $$a-1$$
- $$-a-1$$
- $$-\frac{1}{a+1}$$
- $$-\frac{1}{a-1}$$
- $$a+1$$
- $$\frac{a}{a+1}\cdot\frac{a^2-1}{a}$$
- $$a^2+\frac{a^3-1}{1-a}$$
- $$\frac{1-a}{a}:\frac{a^2-1}{a}$$
- $$\frac{a-2}{a-1}-1$$
- Задание 23 из 34
23.
Из всех натуральных чисел, больших 9 и меньших 20, наугад выбрали одно число. Установить соответствие между событием и вероятностью его появления.
Элементы сортировки
- 0.4
- 1
- 0
- 0.3
- 0.2
- выбранное число будет простым
- выбранное число состоит из двух цифр
- выбранное число будет делителем числа 5
- сумма цифр выбранного числа будет делиться на 3
- Задание 24 из 34
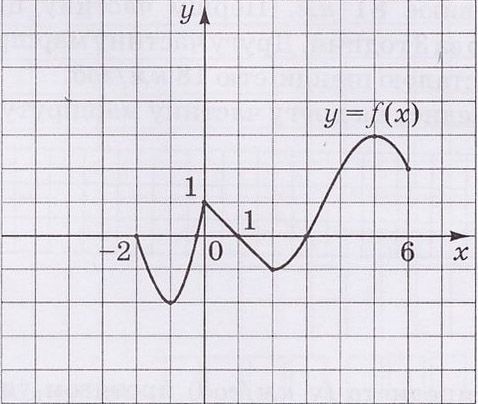
24.
На рисунке изображен график функции $$y=f(x),$$ определенной на отрезке $$[-2;6].$$ Установите соответствие между утверждениями и уравнениями прямой, для которой это утверждение является правильным.

Элементы сортировки
- $$y=3+x$$
- $$y=2$$
- $$y=3-x$$
- $$y=1-x$$
- $$y=1$$
- прямая не пересекает график функции $$y=f(x)$$
- прямая является касательной, проведенной к графику функции $$y=f(x)$$ в точке с абсциссой $$x=5$$
- прямая пересекает график функции $$y=f(x)$$ в точке с абсциссой $$x=3$$
- прямая имеет с графиком функции $$y=f(x)$$ не менее трех общих точек на отрезке $$[0;2]$$
- Задание 25 из 34
25.
Длина маршрута велосипедиста равна 81 км. Первую часть этого маршрута он проехал с постоянной скоростью за 3 часа. Вторую часть маршрута длиной 36 км велосипедист проехал с постоянной скоростью 18 км/ч.
1. Сколько времени (в часах) потратил велосипедист на вторую часть маршрута?
2. Какой была средняя скорость велосипедиста (в км/ч) на протяжении всего маршрута?
- 1. Ответ: (2) 2. Ответ: (16,2, 16.2)
- Задание 26 из 34
26.
Площадь ромба равна $$10.8$$ см2, а площадь круга, вписанного в этот ромб – $$2.25\pi$$ см2.
1. Определите длину радиуса круга, вписанного в ромб (в см).
2. Вычислить длину стороны ромба (в см).
- 1. Ответ: (1.5, 1,5) 2. Ответ: (3.6, 3,6)
- Задание 27 из 34
27.
Вычислить $$\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}}5\text{ctg}x\sin x dx.$$
- Задание 28 из 34
28.
Решить неравенство $$(18+2x)^2(x^2+8x+15)\leqslant 0.$$ В ответе запишите сумму всех его целых решений.
- Задание 29 из 34
29.
Вычислить значение выражения $$(\sqrt[6]{27}-\sqrt[4]{100})\cdot(\sqrt[6]{27}+\sqrt[4]{100}).$$
- Задание 30 из 34
30.
Решить систему уравнений $$\left\{\begin{matrix}\sqrt{y-7x+33}=x\\ 4x-y=5\end{matrix}\right.$$
Если система имеет одно решение $$(x_0;y_0),$$ то в ответ запишите произведение $$x_0\cdot y_0.$$ Если система имеет два решения $$(x_1;y_1)$$ и $$(x_2;y_2),$$ то в ответ запишите наибольшее из произведений $$x_1\cdot y_1$$ и $$x_2\cdot y_2.$$
- Задание 31 из 34
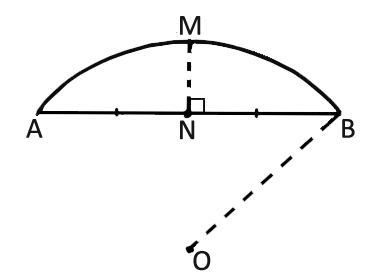
31.
На рисунке схематично изображен выпуклый мост, имеющий форму дуги $$AMB$$ окружности с центром в точке $$O.$$ $$MN$$ – серединный перпендикуляр к $$AB,$$ $$MN=3$$ м. Определить длину радиуса $$OB$$ (в метрах), если длина отрезка $$AB$$ равна 12 м.

- Задание 32 из 34
32.
Областью определения периодической функции $$y=f(x)$$ с периодом $$T=9$$ есть множество всех действительных чисел. На промежутке $$(-5;4]$$ эта функция задана формулой $$f(x)=19-x^3.$$ Вычислить значение $$f(5).$$
- Задание 33 из 34
33.
В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ $$(BC\parallel AD).$$ Боковая грань $$SBC,$$ площадь которой равна $$24.4$$ см2, перпендикулярна к плоскости основания пирамиды. Точка $$M$$ – середина ребра $$SB.$$ Плоскость $$(MAD)$$ пересекает ребро $$SC$$ в точке $$N.$$ Определите длину отрезка $$MN$$ (в см), если объем пирамиды равен $$152$$ см2, а площадь ее основания – $$57$$ см2.
- Задание 34 из 34
34.
Найти наименьшее значение параметра $$a,$$ при котором уравнение $$2^{\sin^2(2\pi x+\frac{5\pi}{4})}=\frac{4}{(x-a)^2-6(x-a)+13}$$ имеет положительный корень.