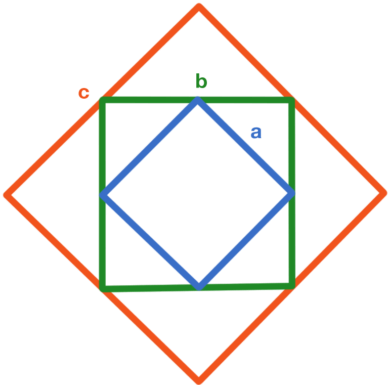
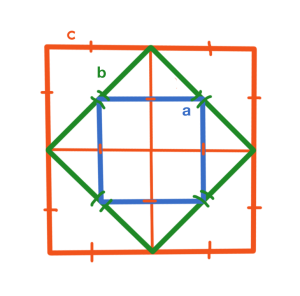
Квадрат со стороной $$b$$ вписан в квадрат со стороной $$c$$ и в него вписан еще один квадрат со стороной $$a.$$ Вершины вписанных квадратов лежат на середине сторон квадратов, в которые они вписаны (см. рисунок). Площадь самого маленького квадрата – 25, какова площадь самого большого квадрата?
Решение
Существует несколько способов решения данной задачи. Разберем два из них:
1. основываясь на знаниях учеников 5 класса о площадях квадрата и треугольника;
2. если ученики 5 класса еще не знают формул площадей.
1 способ
Сначала рассмотрим два внутренних квадрата (средний и маленький).
Проведем диагональ в самом маленьком квадрате, получим прямоугольный треугольник (одна из вершин треугольника совпадает с вершиной квадрата). Из вершины прямого угла проведем высоту на сторону, лежащую напротив этого угла. Очевидно, что полученная высота равна $$\frac{b}{2},$$ противолежащая сторона равна $$b,$$ а стороны при угле в $$90^{\circ}$$ равны по $$a$$ (из условия задачи + см. рисунок).
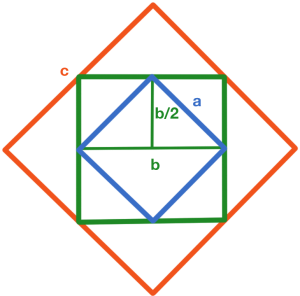
Площадь полученного треугольника найдем двумя способами:
1. Так как треугольник прямоугольный, то его площадь можно найти, перемножив длины сторон при прямом угле и разделив полученное произведение на 2. То есть $$S_{\triangle}=\frac{a^2}{2}.$$
2. Используя формулу площади произвольного треугольника, найдем площадь, перемножив сторону и опущенную к ней высоту, разделив затем полученное произведение на 2. То есть $$S_{\triangle}=b\cdot\frac{b}{2}\cdot\frac{1}{2}=\frac{b^2}{4}.$$
Приравняв площади, получим:
$$\frac{b^2}{4}=\frac{a^2}{2},$$ отсюда $$b^2=2a^2.$$ То есть площадь вписанного квадрата, вершины которого делят стороны описанного квадрата пополам, в два раза меньше площади описанного квадрата.
Теперь рассмотрим средний и большой квадраты, выполнив те же действия, как для малого и среднего квадратов (см. рисунок).
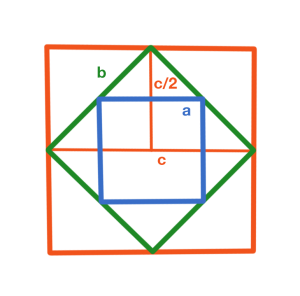
Пользуясь выводом для случая малого и среднего квадратов, получим:
$$c^2=2b^2.$$
Или $$c^2=2b^2=2\cdot2a^2=4a^2=4\cdot25=100$$
Ответ: 100
2 способ
Данный способ основан на равенстве площадей треугольников (см. рисунки ниже для малого и среднего квадратов и для среднего и большого квадратов).
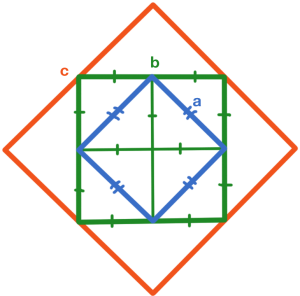
Очевидно, что малый квадрат состоит из 4-х равных треугольников, а средний – из 8-ми. То есть площадь малого квадрата в 2 раза меньше площади среднего.
Аналогично предыдущему площадь среднего квадрата в 2 раза меньше площади большого. Значит площадь большего квадрата в 4 раза больше площади меньшего.
Соответственно площадь большого квадрата равна 100.
Ответ: 100.