Онлайн тест составлен на основе заданий пробного тестирования внешнего независимого оценивания 2013 по математике.
Тест длится 1 час. Не торопитесь. Для перехода к нужному заданию Вы можете воспользоваться блоком навигации вверху теста. После прохождения теста Вы сможете ознакомиться с полученными результатами и правильным решением заданий.
Навигация (только номера заданий)
0 из 12 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
Информация
Желаем удачи в прохождении теста!
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 12
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
Рубрики
- Нет рубрики 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- С ответом
- С отметкой о просмотре
- Задание 1 из 12
1.
Количество баллов: 1Расположите в порядке возростания числа $$\frac{1}{9};\,0.1;\,0.11.$$
Правильно
Неправильно
Для того, чтобы расположить числа в порядке возрастания, необходимо сравнить их. Переведем дроби в обыкновенные.
Вспомним свойства:
- При одинаковых числителях больше та дробь, у которой знаменатель меньше.
- При одинаковых знаменателях больше та дробь, у которой числитель больше.
$$\frac{1}{9}>\frac{1}{10}=0.1$$
$$0.11=\frac{11}{100}>\frac{10}{100}=\frac{1}{10}=0.1$$ (хотя для десятичных дробей сразу видно, что число $$0.11$$ расположено на числовой оси правее числа $$0.1$$)
$$0.11=\frac{11}{100}=\frac{99}{900}<\frac{100}{900}=\frac{1}{9}$$
Значит $$0.1<0.11<\frac{1}{9}$$
$$0.1;\,0.11;\,\frac{1}{9}$$ – расположены в порядке возрастания.
- Задание 2 из 12
2.
Количество баллов: 1На рисунке изображен график функции $$y=f(x)$$, которая определена на отрезке $$[-4;3].$$ Укажите область значений этой функции.
 Правильно
Правильно
Неправильно
Область значений функции $$y=f(x)$$ — множество значений, которые принимает переменная $$y$$ в результате применения функции. Из графика видно, что $$y\in[-1; 2].$$
- Задание 3 из 12
3.
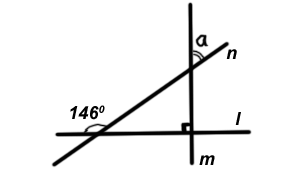
Количество баллов: 1Прямая $$n$$ пересекает перпендикулярные прямые $$l$$ и $$m$$ (см. рисунок). Определите градусную меру угла $$a$$.
 Правильно
Правильно
Неправильно
Воспользуемся свойствами смежных и вертикальных углов, суммой углов прямоугольного треугольника
$$a=90^{\circ}-(180^{\circ}-146^{\circ})=56^{\circ}$$
- Задание 4 из 12
4.
Количество баллов: 1Диагонали параллелограмма $$ABCD$$ пересекаются в точке $$O$$ (см. рисунок). Укажите правильное векторное равенство.
 Правильно
Правильно
Неправильно
$$\vec{CO}=\frac{1}{2}\vec{CA}=-\frac{1}{2}\vec{AC}=-\frac{1}{2}\left (\vec{AB}+\vec{AD} \right )$$
- Задание 5 из 12
5.
Количество баллов: 1Решите неравенство $$2x\geqslant x^2.$$
Правильно
Неправильно
$$x^2-2x\leqslant 0$$
$$x(x-2)\leqslant 0$$
Решаем методом интервалов

$$x\in [0;2]$$
- Задание 6 из 12
6.
Количество баллов: 1Вычислить $$\sqrt{2}\cdot\sqrt{0.08}.$$
Правильно
Неправильно
Используем свойства корней
$$\sqrt{2}\cdot\sqrt{0.08}=\sqrt{2\cdot0.08}=\sqrt{0.16}=\sqrt{(0.4)^2}=0.4$$
- Задание 7 из 12
7.
Количество баллов: 1Упростите выражение $$\frac{9-x^2}{x^2+6x+9}.$$
Правильно
Неправильно
Выполним преобразования, применив формулы сокращенного умножения
$$\frac{9-x^2}{x^2+6x+9}=\frac{(3-x)(3+x)}{(x+3)^2}=\frac{3-x}{x+3}$$
- Задание 8 из 12
8.
Количество баллов: 1Диаметр основания конуса равен 6 см, а площадь его боковой поверхности – $$24\pi$$ см2. Найдите длину образующей конуса.
Правильно
Неправильно
Диаметр основания конуса равен 6 см, значит радиус равен 3 см.
Площадь боковой поверхности конуса находится по формуле
$$S=\pi\cdot R\cdot l$$, где $$R$$ – радиус основания конуса, $$l$$ – образующая конуса. Так как площадь боковой поверхности конуса равна $$24\pi$$ см2, то образующая равна
$$l=\frac{S}{R\pi}=\frac{24\pi}{3\pi}=8$$ см.
- Задание 9 из 12
9.
Количество баллов: 4В лаборатории имеется два сплава меди с оловом: первый, массой 50 кг, содержит 10% меди; второй, массою 100 кг, – содержит 25% меди. Для каждого вопроса подберите правильный ответ.
Элементы сортировки
- 5
- 30
- 20
- 25
- 15
- Сколько килограммов меди содержится в первом сплаве?
- Сколько килограммов меди содержится в двух сплавах вместе?
- Если из этих сплавов составить новый сплав, то сколько процентов меди будет содержать этот сплав?
- Сколько килограммов второго сплава необходимо добавить к первому, чтобы создать сплав, содержащий 15% меди?
Правильно
Неправильно
1) Сколько килограммов меди содержится в первом сплаве?
Так как масса первого сплава равна 50 кг и в нем содержится 10% меди, то
$$x_1$$ кг меди – 10%
50 кг первого сплава – 100%
Получили пропорцию
$$\frac{x_1}{50}=\frac{10\%}{100\%}\Rightarrow x_1=50\cdot 0.1=5$$ кг.
2) Сколько килограммов меди содержится в двух сплавах одновременно?
Сначала найдем массу меди во втором сплаве, а затем массу меди в двух сплавах одновременно.
$$x_2$$ кг меди – 25%
100 кг второго сплава – 100%
$$\frac{x_2}{100}=\frac{25\%}{100\%}\Rightarrow x_2=100\cdot 0.25=25$$ кг
Так как масса меди в первом сплаве равна 5 кг (см. 1), то
$$5+25=30$$ кг – общая масса меди в двух сплавах одновременно
3) Если из данных сплавов образовать новый сплав, то сколько процентов меди будет содержать новый сплав?
Общая масса меди в двух сплавах равна 30 кг (см. 2)
Общая масса двух сплавов равна 50 + 100 = 150 кг – масса нового сплава.
30 кг меди – p%
150 кг нового сплава – 100%
$$\frac{30}{150}=\frac{p\%}{100\%}\Rightarrow p=\frac{1}{5}\cdot 100=20$$
4) Сколько килограммов второго сплава необходимо прибавить к первому, чтобы получился сплав, содержащий 15% меди?
Пусть необходимо прибавить $$y$$ кг второго сплава с массой меди в нем, равной $$0.25y$$ кг (по условию во втором сплаве 25% меди).
$$5+0.25y$$ кг меди – 15%
$$50+y$$ кг сплава – 100%
$$\frac{5+0.25y}{50+y}=\frac{15\%}{100\%}$$
$$5+0.25y=0.15\cdot(50+y)$$
$$0.25y-0.15y=7.5-5$$
$$0.1y=2.5$$
$$y=25$$ кг
- Задание 10 из 12
10.
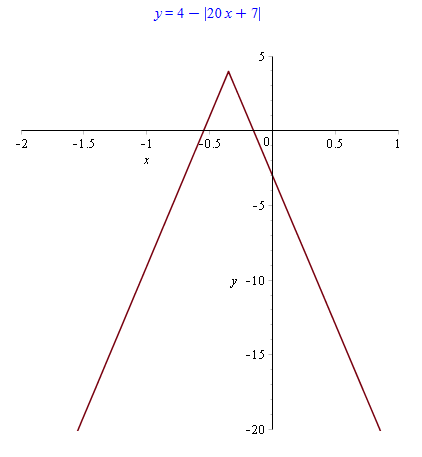
Количество баллов: 2При каком значении $$x$$ функция $$y=4-|20x+7|$$ достигает наибольшего значения?
Правильно
Неправильно
Воспользуемся определением модуля и преобразуем функцию
$$y=4-|20x+7|=\left[\begin{matrix} 4-(20x+7), 20x+7\geqslant 0\\ \\ 4-(-20x-7), 20x+7< 0 \end{matrix}\right.=\left[\begin{matrix} -20x-3, x\geqslant -\frac{7}{20}\\ \\ 20x+11, x< -\frac{7}{20} \end{matrix}\right.$$
$$y=20x+11$$ возрастающая функция, а $$y=-20x-3$$ – убывающая.
Значит функция $$y=4-|20x+7|$$ возрастает при $$x\in(-\infty;-\frac{7}{20})$$ и убывает при $$x\in[-\frac{7}{20};\infty)$$, а при $$x=-\frac{7}{20}=-0.35$$ принимает наибольшее значение (см. рисунок).
График функции $$y=4-|20x+7|$$

Ответ: $$-0.35$$.
- Задание 11 из 12
11.
Количество баллов: 2Вычислить $$\log_{b}a,$$ если $$\log_{3}a=8,\,\log_{3}b=5.$$
Правильно
Неправильно
Воспользуемся формулой перехода к новому основанию и получим
$$\log_{b}a=\frac{\log_{3}a}{\log_{3}b}=\frac{8}{5}=1.6$$
Ответ: 1.6.
- Задание 12 из 12
12.
Количество баллов: 2Найдите наименьшее целое значение параметра $$a,$$ при котором уравнение $$\sqrt{x^2-5x}+\sqrt{x^2-9x+20}=\sqrt{a}\cdot\sqrt{x-5}$$ имеет два корня.
Правильно
Неправильно
Преобразуем левую часть. В первом подкоренном выражении вынесем общий множитель за скобки. Для второго используем формулу разложения квадратного трехчлена на множители, найдя его корни по теореме Виета.
$$\sqrt{x(x-5)}+\sqrt{(x-4)(x-5)}=\sqrt{a}\cdot\sqrt{x-5}$$
ОДЗ:
$$\left\{\begin{matrix} x(x-5) & \geqslant & 0\\ (x-4)(x-5) & \geqslant & 0\\ x-5& \geqslant& 0\\ a& \geqslant & 0 \end{matrix}\right.\Rightarrow x\geqslant5,\;a\geqslant0$$
Применим свойство корней (корень произведения)
$$\sqrt{x}\cdot\sqrt{x-5}+\sqrt{x-4}\cdot\sqrt{x-5}=\sqrt{a}\cdot\sqrt{x-5}$$
Вынесем общий множитель за скобки
$$\sqrt{x-5}\cdot(\sqrt{x}+\sqrt{x-4}-\sqrt{a})=0$$
Произведение равно нулю, когда хотя бы один из сомножителей равен нулю, значит
$$\sqrt{x-5}=0$$ или $$\sqrt{x}+\sqrt{x-4}-\sqrt{a}=0$$
$$x=5$$ или $$\sqrt{x}+\sqrt{x-4}=\sqrt{a}$$
$$x=5$$ является корнем уравнения и не зависит от параметра $$a$$
Рассмотрим уравнение $$\sqrt{x}+\sqrt{x-4}=\sqrt{a}$$
Левая и права часть уравнения неотрицательны ($$\sqrt{}$$ $$\geqslant 0$$). Возведем в квадрат обе части уравнения
$$\left (\sqrt{x}+\sqrt{x-4} \right )^2=\left (\sqrt{a} \right )^2$$
Раскроем скобки, используя свойства корней и формулу квадрата суммы
$$x+x-4+2\sqrt{x(x-4)}=a$$
$$2\sqrt{x(x-4)}=a+4-2x$$
Левая часть неотрицательна, значит и правая часть должна быть неотрицательной. Получили дополнительное условие $$a+4-2x\geqslant 0\Rightarrow x\leqslant \frac{a+4}{2}$$
C учетом ОДЗ
$$5\leqslant x\leqslant \frac{a+4}{2}\Rightarrow \frac{a+4}{2}\geq 5\Rightarrow a\geq 6$$
Возведем в квадрат обе части уравнения
$$\left (2\sqrt{x(x-4)} \right )^2=\left (a+4-2x \right )^2$$
$$4x(x-4)=(a+4)^2+4x^2-4x(a+4)$$
$$4x^2-16x=(a+4)^2+4x^2-16x-4ax$$
$$4ax=(a+4)^2$$
$$x=\frac{(a+4)^2}{4a}$$
Найдем наименьшее целое значение параметра, при котором найденный $$x$$ является корнем уравнения
$$\frac{(a+4)^2}{4a}\geqslant 5$$
$$\frac{(a+4)^2}{4a}-5\geqslant 0$$
$$\frac{(a+4)^2-20a}{4a}\geqslant 0$$
$$\frac{a^2+16+8a-20a}{4a}\geqslant 0$$
$$\frac{a^2-12a+16}{4a}\geqslant 0$$
$$a\geqslant 6\Rightarrow 4a>0\Rightarrow a^2-12a+16\geqslant 0$$
Рассмотрим $$a^2-12a+16=0$$
Найдем корни (воспользуемся формулой дискриминанта для четного коэффициента при первой степени)
$$D_1=36-16=20=2^2\cdot5$$
$$a_{1,2}=6\pm2\sqrt{5}$$
$$\left [a-(6-2\sqrt{5}) \right ]\cdot\left [a-(6+2\sqrt{5}) \right ]\geqslant 0$$
$$a\geqslant 6\Rightarrow a-(6-2\sqrt{5}) >0\Rightarrow a-(6+2\sqrt{5})\geqslant 0\Rightarrow a\geqslant 6+2\sqrt{5}$$
$$6+2\sqrt{5} \approx 10.47$$
Значит наименьшее целое значение параметра $$a=11$$, при котором исходное уравнение имеет два корня
$$x_1=5,\;x_2=\frac{(11+4)^2}{4\cdot11}=\frac{225}{44}=5\frac{5}{44}$$
Ответ: $$a=11.$$