Задание 15
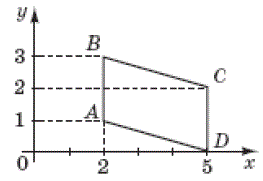
Обчисліть площу чотирикутника $$ABCD$$ (див. рисунок), сторони якого паралельні вісі $$Oy.$$
| А | Б | В | Г | Д |
| 10 | 5 | 3 | 6 | 7 |
Решение:
$$ABCD$$ – параллелограмм. $$AB=CD=2, CE=3$$ – высота.
$$S=AB\cdot CE=2\cdot 3=6$$
Ответ: Г.
Задание 16
Якому з наведених нижче проміжків належить корінь рівняння $$5^{x+2}=\left (\frac{1}{125} \right )^x?$$
| А | Б | В | Г | Д |
| $$(-3;-2]$$ | $$(-2;-1]$$ | $$(-1;0]$$ | $$(0;1]$$ | $$(1;3]$$ |
Решение:
$$5^{x+2}=\left (\frac{1}{5^3} \right )^x\Rightarrow 5^{x+2}=5^{-3x}\Rightarrow x+2=-3x\Rightarrow x=-\frac{1}{2} \in (-1;0]$$
Ответ: В.
Задание 17
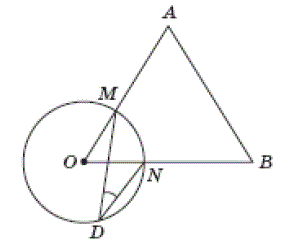
На рисунку зображено коло з центром у точці $$O$$ і рівносторонній трикутник $$AOB,$$ що перетинає коло в точках $$M$$ і $$N$$. Точка $$D$$ належить колу. Знайдіть градусну міру кута $$MDN$$.
| А | Б | В | Г | Д |
| $$15^{\circ}$$ | $$30^{\circ}$$ | $$45^{\circ}$$ | $$60^{\circ}$$ | $$120^{\circ}$$ |
Решение:
Треугольник $$AOB$$ равносторонний, значит углы $$AOB, OBA$$ и $$BAO$$ равны по $$60^{\circ}.$$ Угол $$AOB$$ – центральный угол, опирающийся на дугу $$MN$$. Искомый угол $$MDN$$ – вписаный угол, опирающийся на ту же дугу MN.
Вписаный угол равен половине центрального угла, опирающегося на ту же дугу.
Значит угол $$MDN$$ равен $$30^{\circ}.$$
Ответ: Б.
Задание 18
Функція $$y=f(x)$$ є спадною на проміжку $$\left (-\infty;\infty \right ).$$ Укажіть правильну нерівність.
| А | Б | В | Г | Д |
| $$f(1)>f(-1)$$ | $$f(1) < f(8)$$ | $$f(1)>f(0)$$ | $$f(-1) < f(0)$$ | $$f(1)>f(10)$$ |
Решение:
Воспользуемся определением убывающей функции.
$$y=f(x)$$ убывает, если $$f(x_{1})>f(x_{2})$$ при $$x_1 < x_{2}.$$
Данному условию удовлетворяет $$f(1)>f(10).$$
Ответ: Д.
Задание 19
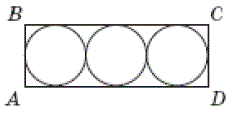
У прямокутник ABCD вписано три круги одного й того самого радіуса (див. рисунок). Визначте довжину сторони BC, якщо загальна площа кругів дорівнює $$3\pi.$$
| А | Б | В | Г | Д |
| 2 | 3 | 6 | 9 | 18 |
Решение:
$$S_{kp}=\pi R^2$$
$$S=3\pi =3S_{kp}=3\pi R^2\Rightarrow 3\pi=3\pi R^2\Rightarrow R=1$$
$$BC=6R=6$$
Ответ: В.
Задание 20
О шостій годині ранку визначено температуру на десяти метеостанціях. Отримані дані відображено в таблиці.
| Температура в градусах | 1 | 3 | 4 | x |
| Кількість метеостанцій | 2 | 3 | 4 | 1 |
Визначте $$x$$, якщо середнє арифметичне всіх цих даних дорівнює $$3.5^{\circ}.$$
| А | Б | В | Г | Д |
| $$x=5$$ | $$x=6$$ | $$x=7$$ | $$x=8$$ | $$x=9$$ |
Решение:
$$\frac{2\cdot1^{\circ}+3\cdot3^{\circ}+4\cdot4^{\circ}+1\cdot x^{\circ}}{2+3+4+1}=\frac{27^{\circ}+x^{\circ}}{10}=3.5^{\circ}$$
$$27^{\circ}+x^{\circ}=35^{\circ}\Rightarrow x^{\circ}=8^{\circ}$$
Ответ: Г.
Задание 21
У трикутнику ABC: AB=31 см, BC=15 см, AC=26 см. Пряма а, паралельна стороні АВ, перетинає ВС і АС у точках M і N відповідно. Обчисліть периметр трикутника MNC, якщо MC=5 см.
| А | Б | В | Г | Д |
| 15 см | 24 см | 48 см | 21 см | 26 см |
Решение:
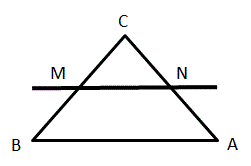
$$\triangle ABC\sim \triangle NMC$$ (по трем углам)
$$\frac{MC}{BC}=\frac{NC}{AC}=\frac{MN}{BA}$$
$$NC=\frac{MC\cdot AC}{BC}=\frac{5\cdot 26}{15}=\frac{26}{3}, MN=\frac{BA\cdot MC}{BC}=\frac{31\cdot 5}{15}=\frac{31}{3}$$
$$P=MC+CN+MN=5+\frac{26}{3}+\frac{31}{3}=\frac{15+26+31}{3}=\frac{72}{3}=24$$
Ответ: Б.