Задание 29
Обчисліть значення виразу $$\frac{3\sqrt{2}-5}{\sqrt{2}-1}+\frac{\sqrt{24}-\sqrt{300}}{\sqrt{3}}.$$.
Решение:
$$\frac{3\sqrt{2}-5}{\sqrt{2}-1}+\frac{\sqrt{24}-\sqrt{300}}{\sqrt{3}}=\frac{3\sqrt{2}-5}{\sqrt{2}-1}+\frac{2\sqrt{2}\cdot\sqrt{3}-10\sqrt{3}}{\sqrt{3}}=$$
$$=\frac{3\sqrt{2}-5}{\sqrt{2}-1}+2\sqrt{2}-10=\frac{3\sqrt{2}-5+4-2\sqrt{2}-10\sqrt{2}+10}{\sqrt{2}-1}=$$
$$=\frac{9-9\sqrt{2}}{\sqrt{2}-1}=\frac{-9(\sqrt{2}-1)}{\sqrt{2}-1}=-9$$
Ответ: -9.
Задание 30
Матеріальна точка рухається за законом $$s(t)=2t^2+3t,$$ де $$S$$ вимірюється в метрах, а $$t$$ у секундах. Знайдіть значення $$t$$ (у секундах), при якому миттєва швидкість матеріальної точки дорівнює 76 м/с.
Решение:
$$s^{\prime}$$ – мгновенная скорость материальной точки.
$$s^{\prime}(t)=4t+3\Rightarrow 4t+3=76\Rightarrow 4t=73\Rightarrow t=18.25$$
Ответ: 18.25
Задание 31
У відділі працює певна кількість чоловіків і жінок. Для анкетування навмання вибрали одного із співробітників. Імовірність того, що це чоловік, дорівнює $$\frac{2}{7}.$$ Знайдіть відношення кількості жінок до кількості чоловіків, які працюють у цьому відділі.
Решение:
Вероятность события $$A:P(A)=\frac{m}{n},$$ где $$m$$ – число благоприятных исходов, $$n$$ – число всех исходов. Значит количество мужчин равно $$2,$$ а количество женщин равно $$7-2=5.$$
Отношение количества женщин к количеству мужчин равно $$\frac{5}{2}=2.5$$
Ответ: 2.5.
Задание 32
Двоє робітників, працюючи разом, можуть скосити траву на ділянці за 2 години 6 хвилин. Скільки часу (у годинах) витратить на скошування трави на цій ділянці другий робітник, працюючи самостійно, якщо йому потрібно на виконання цього завдання на 4 години більше, ніж першому робітникові?
Решение:
Пусть второму работнику для выполнения всего задания понадобится $$x$$ часов, тогда первому – $$(x-4)$$ часов. Вместе им понадобится 2 часа 6 минут, т.е. $$2\frac{6}{60}=2.1$$ часа.
$$\frac{1}{x-4}$$ – часть работы, которую выполнит первый рабочий.
$$\frac{1}{x}$$ – часть работы, которую выполнит второй рабочий.
$$\frac{1}{2.1}$$ – часть работы, которую выполнят вместе.
Составим уравнение:
$$\frac{1}{x-4}+\frac{1}{x}=\frac{1}{2.1} \sim \frac{1}{x-4}+\frac{1}{x}=\frac{10}{21}$$
Перенесем в одну сторону, приведем к общему знаменателю и запишем под одной дробью:
$$\frac{21\cdot x+21\cdot (x-4)-10\cdot x\cdot (x-4)}{21\cdot x\cdot (x-4)}=0$$
Раскроем скобки и запишем числитель равен нулю, а знаменатель не равен нулю:
$$21x+21x-84-10x^2+40x=0,21\cdot x\cdot (x-4)\neq0$$
Приведем подобные слагаемые:
$$10x^2-82x+84=0,x\neq 0, x\neq 4$$
Разделим обе части уравнения на 2:
$$5x^2-41x+42=0$$
$$D=41^2-4\cdot5\cdot42=1682-840=841=29^2$$
$$x_{1}=\frac{41-29}{10}=1.2, x_{2}=\frac{41+29}{10}=7$$
$$x_{1}=1.2$$ – посторонний корень (иначе $$x-4<0)$$
Значит второму рабочему понадобится 7 часов на самостоятельное выполнение задания.
Ответ: 7.
Задание 33
У чотирикутну піраміду, в основі якої лежить рівнобічна трапеція з бічною стороною 13 см і основами 18 см і 8 см, вписано конус. Знайдіть площу бічної поверхні конуса $$S$$ (у см2), якщо всі бічні грані піраміди нахилені до площини основи під кутом $$60^{\circ}.$$ У відповіді запишіть значення $$\frac{S}{\pi}.$$
Решение:
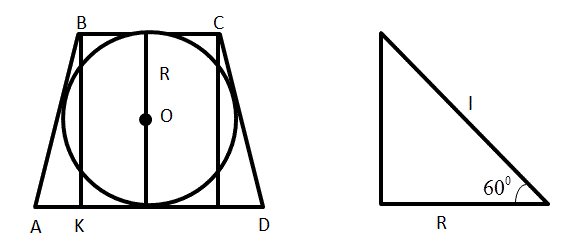
Площадь боковой поверхности конуса $$S=\pi R l,$$ где $$l$$ – образующая конуса, $$R$$ – радиус основания.
$$ABCD$$ – равнобокая трапеция: $$AD=18,BC=8, AB=CD=13$$ (см. рисунок слева)
Проведем высоты из точек $$B$$ и $$C$$ на $$AD.$$ $$BK=2R$$ – высота трапеции и катет прямоугольного треугольника $$AKB.$$ $$AK=\frac{AD-BC}{2}=\frac{18-8}{2}=5.$$
$$BK=\sqrt{AB^2-AK^2}=\sqrt{13^2-5^2}=\sqrt{169-25}=\sqrt{144}=12$$
$$R=\frac{BK}{2}=6$$
Из прямоугольного треугольника (см. рисунок справа) $$l=\frac{R}{\cos 60^{\circ}}=6:\frac{1}{2}=12$$
$$\frac{S}{\pi}=R\cdot l=6\cdot 12=72$$
Ответ: 72.
Задание 34
На рисунку зображено графік функції $$y=f(x),$$ що визначена на проміжку $$\left ( -\infty;\infty \right )$$ і має лише три нулі. Розв’яжіть систему $$\left\{\begin{matrix} f(x)&\geqslant 0 \\ x^2+x-6&>0. \end{matrix}\right.$$
У відповіді запишіть суму всіх цілих розв’язків системи.
Решение:

$$f(x)\geqslant 0\Rightarrow x\in [-1;6]\cup \left \{ 9 \right \}$$
$$x^2+x-6>0\sim (x+3)(x-2)>0$$ (из уравнения $$x^2+x-6=0$$ по теореме Виета: $$x_{1}=-3,x_{2}=2)$$

$$x\in(-\infty;-3)\cup(2;\infty)$$
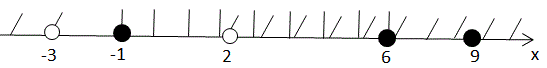
$$x\in(2;6]\cup\left \{ 9 \right \}$$
Сумма всех целых решений: $$3+4+5+6+9=27$$
Ответ: 27.
Задание 35
Знайдіть найменше значення $$a,$$ при якому має розв’язки рівняння $$\frac{1}{2}(\sin x+\sqrt{3}\cos x)=6-5a-2a^2$$
Решение:
$$\frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x=6-5a-2a^2$$
$$\cos 60^{\circ}\sin x+\sin 60^{\circ}\cos x=6-5a-2a^2$$
$$\sin (60^{\circ}+ x)=6-5a-2a^2$$
Простейшее тригонометрическое уравнение:
$$\sin x=a, |a|\leqslant 1$$
$$x=(-1)^k \arcsin a+\pi k,k\in\mathbb{Z}$$
$$|6-5a-2a^2|\leqslant 1$$
$$\left\{\begin{matrix} 6-5a-2a^2\leqslant 1\\ 6-5a-2a^2\geqslant -1 \end{matrix}\right.$$
$$\left\{\begin{matrix} 2a^2+5a-5\geqslant 0\\ 2a^2+5a-7 \leqslant 0 \end{matrix}\right.$$
$$2a^2+5a-5= 0, D=25+40=65,a_{1,2}=\frac{-5\pm \sqrt{65}}{4}$$
$$2a^2+5a-7 =0, D=25+56=81,a_{3,4}=\frac{-5\pm 9}{4}$$
$$a_{1}=\frac{-5-\sqrt{65}}{4}>-3.5,a_{2}=\frac{-5+\sqrt{65}}{4}<1, a_{3}=-3.5,a_{4}=1$$
$$\left\{\begin{matrix} (a-\frac{-5-\sqrt{65}}{4})(a-\frac{-5+\sqrt{65}}{4})\geqslant 0\\ (a+3.5)(a-1) \leqslant 0 \end{matrix}\right.$$
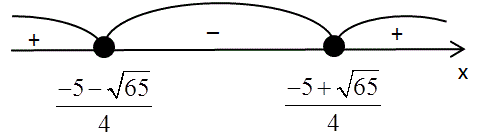
$$a\in \left ( -\infty; \frac{-5-\sqrt{65}}{4}\right ]\cup\left [ \frac{-5+\sqrt{65}}{4};\infty \right )$$
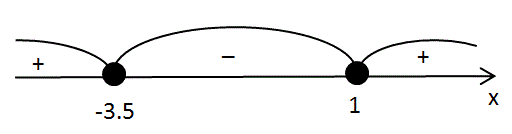
$$a\in[-3.5;1]$$
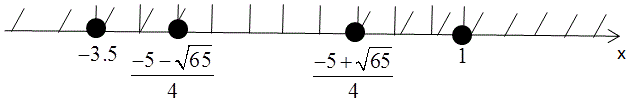
$$a\in[-3.5;\frac{-5-\sqrt{65}}{4}]\cup[\frac{-5+\sqrt{65}}{4};1]$$
$$a_{min}=-3.5$$
Ответ: -3.5.