Задание 9
Якщо $$a=1-\frac{b}{c},$$ то $$b=$$
| А | Б | В | Г | Д |
| $$c(1-a)$$ | $$c(a-1)$$ | $$\frac{c}{1-a}$$ | $$\frac{1-a}{c}$$ | $$1-ac$$ |
Решение:
$$\frac{b}{c}=1-a\Rightarrow b=c(1-a)$$
Ответ: А.
Задание 10
Укажіть правильну нерівність.
| А | Б | В | Г | Д |
| $$\frac{3}{8}>\frac{5}{8}$$ | $$\frac{7}{2}<\frac{7}{3}$$ | $$\frac{8}{9}>\frac{9}{8}$$ | $$\frac{5}{6}>\frac{4}{5}$$ | $$\frac{19}{21}<\frac{6}{7}$$ |
Решение:
Рекомендуем повторить теорию по теме “Дробно-рациональные выражения”. Для двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. Для двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. Для сравнения дробей с разными числителями и знаменателями необходимо привести дроби к общему знаменателю, а затем применить правило для дробей с одинаковыми знаменателями.
$$\frac{3}{8}>\frac{5}{8}$$ – ложно
$$\frac{7}{2}<\frac{7}{3}$$ – ложно
$$\frac{8}{9}>\frac{9}{8}$$ – ложно, так как $$\frac{64}{72}<\frac{81}{72}$$
$$\frac{5}{6}>\frac{4}{5}$$ – верно, так как $$\frac{25}{30}>\frac{24}{30}$$
$$\frac{19}{21}<\frac{6}{7}$$ – ложно, так как $$\frac{19}{21}>\frac{18}{21}$$
Ответ: Г.
Задание 11
Укажіть рисунок, на якому зображено графік парної функції
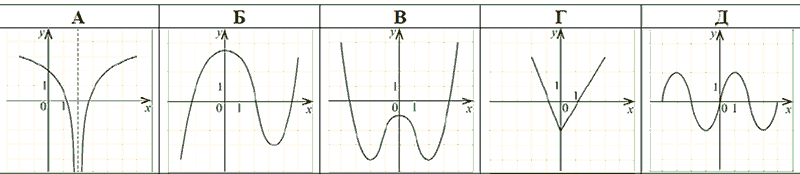
Решение:
График четной функции симметричен относительно оси Оу.
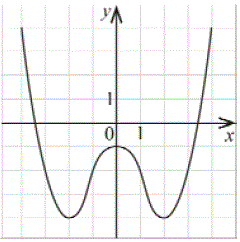
Ответ: В.
Задание 12
Знайдіть вектор $$\vec{c}=2\vec{a}-\vec{b},$$ якщо $$\vec{a}(3;-1;2),\vec{b}(-2;2;5).$$
| А | Б | В | Г | Д |
| $$\vec{c}\left ( 5;-3;-3 \right )$$ | $$\vec{c}\left ( 4;0;-1 \right )$$ | $$\vec{c}\left ( 8;0;-1 \right )$$ | $$\vec{c}\left ( 4;-4;-1 \right )$$ | $$\vec{c}\left ( 8;-4;-1 \right )$$ |
Решение:
$$\vec{c}(2\cdot3+2;2\cdot\left (-1 \right )-2;2\cdot2-5)=\vec{c}\left ( 8;-4;-1 \right )$$
Ответ: Д.
Задание 13
У туриста є 10 однакових за розмірами консервних банок, серед яких 4 банки – з тушкованим м’ясом, 6 банок – з рибою. Під час зливи етикетки відклеїлися. Турист навмання взяв одну банку. Яка ймовірність того, що вона буде з рибою?
| А | Б | В | Г | Д |
| $$\frac{1}{10}$$ | $$\frac{2}{3}$$ | $$\frac{1}{6}$$ | $$\frac{3}{5}$$ | $$\frac{2}{5}$$ |
Решение:
$$P=\frac{m}{n},$$ $$m$$ – число благоприятных исходов, $$n$$ – число всевозможных исходов.
$$m=6,n=10\Rightarrow P=\frac{6}{10}=\frac{3}{5}$$
Ответ: Г.
Задание 14
Знайдіть похідну функції $$y=x^4+3\cos x$$
| А | Б | В | Г | Д |
| $$4x^3+3\sin x$$ | $$4x-3\sin x$$ | $$4x^3-3\sin x$$ | $$\frac{x^5}{5}+3\sin x$$ | $$x^3-3\sin x$$ |
Решение:
$$y’=4x^3-3\sin x$$
Ответ: В.
Задание 15
Укажіть УСІ ПРАВИЛЬНІ твердження.
I. Через точку A, що не належить площині α , можна провести лише одну пряму, паралельну площині α.
II. Через точку A, що не належить площині α , можна провести лише одну площину, паралельну площині α .
III. Через точку A, що не належить площині α , можна провести лише одну пряму, перпендикулярну до площини α.
IV. Через точку A, що не належить площині α , можна провести лише одну площину, перпендикулярну до площини α.
| А | Б | В | Г | Д |
| II | II, III | I, IV | I, III, IV | II, III, IV |
Решение:
Верными являются II и III утверждения.
Ответ: Б.
Задание 16
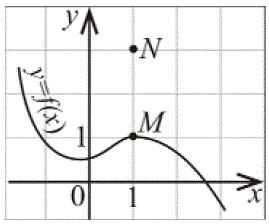
Графік функції $$f(x)$$ проходить через точку $$M(1;1)$$ (див. рисунок). При якому значенні $$a$$ графік функції $$y=f(x)+a$$ проходить через точку $$N(1;3)?$$
| А | $$a=2$$ |
| Б | $$a=-2$$ |
| В | такого значення не існує |
| Г | $$a=\frac{1}{3}$$ |
| Д | $$a=3$$ |
Решение:
Воспользуемся следующим правилом:
Для построения графика функции $$y=f(x)+a,$$ где $$a$$ – некоторое заданное число, если уже построен график функции $$f(x)$$ достаточно передвинуть график функции $$f(x)$$ как твердое тело на $$a$$ единиц вверх, если $$a>0,$$ или на $$|a|$$ единиц вниз, если $$a<0.$$
В нашем случае точка $$N(1;3)$$ расположена на 2 единицы выше точки $$M(1;1),$$ т.е. произойдет смещение графика на 2 единицы вверх. Получили $$a=2.$$
Ответ: А.