Вектором називається направлений відрізок (упорядкована пара точок). До векторів належить також і нульовий вектор, початок і кінець якого співпадають.
Довжиною (модулем) вектора називається відстань між початком і кінцем вектора.
Вектори називаються колінеарними, якщо вони розташовані на одній або на паралельних прямих. Нульовий вектор колінеарний з будь-яким вектором.
Вектори називаються компланарними, якщо існує площина, до якої вони паралельні. Колінеарні вектори завжди компланарні, але не всі компланарні вектори колінеарні.
Вектори називаються рівними, якщо вони колінеарні, однаково направлені і мають однакові модулі.
Усякі вектори можуть бути приведені до загального початку. Із означення рівності векторів випливає, що будь-який вектор має нескінченно багато рівних йому векторів.
Лінійними операціями над векторами називаються операції їх додавання та помноження на число.
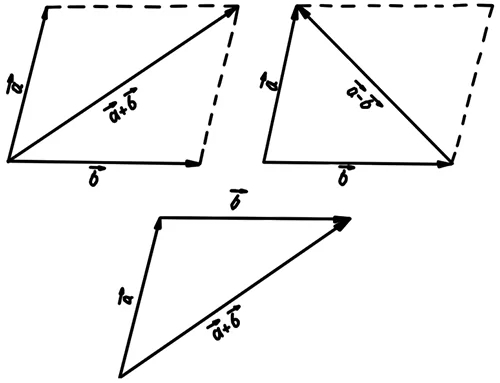
Сумою векторів називається вектор $$\vec{c}=\vec{a}+\vec{b}.$$
Додавання і віднімання векторів:
Добутком вектора $$\vec{a}$$ на число $$k$$ називається вектор $$\vec{b}=k\vec{a},$$ $$|\vec{b}|=k|\vec{a}|,$$ при цьому $$\vec{a}$$ колінеарний $$\vec{b}.$$
Вектор $$\vec{a}$$ однаково спрямований з вектором $$\vec{b}$$ $$(\vec{a}\uparrow\uparrow\vec{b}),$$ якщо $$k>0.$$
Вектор $$\vec{a}$$ протилежно спрямований з вектором $$\vec{b}$$ $$(\vec{a}\uparrow\downarrow\vec{b}),$$ якщо $$k<0.$$
Вектори мають такі властивості:
- $$\vec{a}+\vec{b}=\vec{b}+\vec{a}$$ (комутативність)
- $$\vec{a}+(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+\vec{c}$$
- $$\vec{a}+\vec{0}=\vec{a}$$
- $$\vec{a}+(-1)\cdot\vec{a}=\vec{0}$$
- $$(\alpha\beta)\vec{a}=\alpha (\beta\vec{a})$$ (асоціативність)
- $$(\alpha+\beta )\vec{a}=\alpha\vec{a}+\beta\vec{a}$$ (дистрибутивність)
- $$\alpha(\vec{a}+\vec{b} )=\alpha\vec{a}+\alpha\vec{b}$$
- $$1\cdot\vec{a}=\vec{a}$$
Базисом у просторі називаються будь-які 3 некомпланарні вектори, взяті в певному порядку.
Базисом на площині називаються будь-які 2 неколінеарні вектори, взяті в певному порядку.
Базисом на прямій називається будь-який ненульовий вектор.
Якщо $$\vec{e_{1}},\;\vec{e_{2}},\;\vec{e_{3}}$$ – базис у просторі і $$\vec{a}=\alpha\vec{e_{1}}+\beta\vec{e_{2}}+\gamma\vec{e_{3}}$$, то числа $$\alpha,\;\beta,\;\gamma$$ називаються компонентами або координатами вектора у цьому базисі.
У зв’язку з цим можна записати наступні властивості:
- рівні вектори мають однакові координати;
- при помноженні вектора на число його компоненти також помножаються на це число
$$\lambda\vec{a}=\lambda\left ( \alpha\vec{e_{1}}+\beta\vec{e_{2}}+\gamma\vec{e_{3}} \right )=\left (\lambda\alpha \right )\vec{e_{1}}+\left (\lambda\beta \right )\vec{e_{2}}+\left (\lambda\gamma \right )\vec{e_{3}};$$
- при додаванні векторів додаються їх відповідні компоненти
$$\vec{a}=\alpha_{a}\vec{e_{1}}+\beta_{a}\vec{e_{2}}+\gamma_{a}\vec{e_{3}},\;\vec{b}=\alpha_{b}\vec{e_{1}}+\beta_{b}\vec{e_{2}}+\gamma_{b}\vec{e_{3}};$$
$$\vec{a}+\vec{b}=\left (\alpha_{a}+\alpha_{b} \right )\vec{e_{1}}+\left (\beta_{a}+\beta_{b} \right )\vec{e_{2}}+\left (\gamma_{a}+\gamma_{b} \right )\vec{e_{3}};$$
Вектори $$\vec{a_{1}},…,\vec{a_{n}}$$ називаються лінійно залежними, якщо існує така лінійна комбінація $$k_{1}\vec{a_{1}}+…+k_{n}\vec{a_{n}}=\vec{0},$$ де $$k_{i}\;\;(i=\overline{1,n})$$ одночасно не дорівнюють нулеві, тобто $$k_{1}^2+…+k_{n}^2\neq0.$$
Якщо співвідношення $$k_{1}^2+…+k_{n}^2=0$$ справедливе лише при $$k_{i}=0\;\;(i=\overline{1,n})$$, то вектори називаються лінійно незалежними.
Властивість 1: Якщо серед векторів $$\vec{a_{i}}\;\;(i=\overline{1,n})$$ є нульовий, то ці вектори лінійно залежні.
Властивість 2: Якщо в систему лінійно залежних векторів включити один або декілька векторів, то одержана система також буде лінійно залежна.
Властивість 3: Система векторів лінійно залежна тоді і лише тоді, коли будь-який із векторів цієї системи може бути представлений як лінійна комбінація інших векторів цієї системи.
Властивість 4: Будь-які два колінеарних вектори лінійно залежні і, навпаки, будь-які два лінійно залежні вектори колінеарні.
Властивість 5: Будь-які три компланарні вектори лінійно залежні і, навпаки, будь-які три лінійно залежні вектори компланарні.
Властивість 6: Будь-які 4 вектори лінійно залежні.
Зафіксуємо у просторі точку $$O$$ і розглянемо довільну точку $$M$$. Вектор $$\overrightarrow{OM}$$ назвемо радіус – вектором точки $$M$$. Якщо у просторі задати деякий базис, то точці $$M$$ можна співставити деяку трійку чисел – компоненти відповідного радіус-вектора.
Декартовою системою координат у просторі називається сукупність точки і базиса. Точка називається початком координат. Прямі, які проходять через початок координат, називаються осями координат:
- 1-а вісь – вісь абсцис.
- 2-а вісь – вісь ординат.
- 3-я вісь – вісь аплікат.
Для знаходження компонент вектора необхідно із координат його кінця відняти координати початку. Якщо задані точки $$A(x_{A}, y_{A}, z_{A}),\;B(x_{B}, y_{B}, z_{B})$$, то $$\overrightarrow{AB}(x_{B}-x_{A}, y_{B}-y_{A}, z_{B}-z_{A}).$$
Базис називається ортонормованим, якщо його вектори попарно ортогональні і їх модулі дорівнюють одиниці.
Декартова система координат, базис якої ортонормований, називається декартовою прямокутною системою координат.
Приклад.
Задані вектори $$\vec{a}(1;2;3),\;\vec{b}(-1;0;3),\;\vec{c}(2;1;-1),\;\vec{d}(3;2;2)$$ в деякому базисі. Показати, що вектори $$\vec{a},\;\vec{b},\;\vec{c}$$ утворюють базис і знайти координати вектора $$\vec{d}$$ в цьому базисі.
Розв’язування.
Вектори утворюють базис у випадку, коли вони лінійно незалежні, або якщо визначник із їх координат не дорівнює нулю.
$$\begin{vmatrix} 1 & -1 &2 \\ 2& 0& 1\\ 3 & 3 & -1 \end{vmatrix}=\begin{matrix} \\ \rightarrow \\ \; \end{matrix}\begin{vmatrix} -3 & -1 &2 \\ 0& 0& 1\\ 5 & 3 & -1 \end{vmatrix}=-\begin{vmatrix} -3 &-1 \\ 5& 3 \end{vmatrix}=4\neq0$$
Таким чином, вектори лінійно незалежні і $$\vec{d}=\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}$$
$$\left\{\begin{matrix} \alpha a_{1} &+ & \beta b_{1} & + & \gamma c_{1}& = &d_{1} \\ \alpha a_{2} &+ & \beta b_{2} & + & \gamma c_{2}& = &d_{2} \\ \alpha a_{3} &+ & \beta b_{3} & + & \gamma c_{3}& = &d_{3} \end{matrix}\right.$$
Розв’яжемо цю систему способом Крамера.
$$\Delta_{1}=\begin{vmatrix} d_{1} & b_{1} & c_{1}\\ d_{2} & b_{2} & c_{2}\\ d_{3} & b_{3} & c_{3} \end{vmatrix}=\begin{vmatrix} 3 & -1 & 2\\ 2 & 0 & 1\\ 2 & 3 & -1 \end{vmatrix}=0+12-2-0-9-2=-1$$
$$\alpha=\frac{\Delta_{1}}{\Delta}=-\frac{1}{4}$$
$$\Delta_{2}=\begin{vmatrix} a_{1} & d_{1} & c_{1}\\ a_{2} & d_{2} & c_{2}\\ a_{3} & d_{3} & c_{3} \end{vmatrix}=\begin{vmatrix} 1 & 3 & 2\\ 2 & 2 & 1\\ 3 & 2 & -1 \end{vmatrix}=-2+8+9-12-2+6=7$$
$$\beta=\frac{\Delta_{2}}{\Delta}=\frac{7}{4}$$
$$\Delta_{3}=\begin{vmatrix} a_{1} & b_{1} & d_{1}\\ a_{2} & b_{2} & d_{2}\\ a_{3} & b_{3} & d_{3} \end{vmatrix}=\begin{vmatrix} 1 & -1 & 3\\ 2 & 0 & 2\\ 3 & 3 & 2 \end{vmatrix}=0+18-6-0-6+4=10$$
$$\gamma=\frac{\Delta_{3}}{\Delta}=\frac{10}{4}=\frac{5}{2}$$
Отже, координати вектора $$\vec{d}$$ в базисі $$\vec{a},\;\vec{b},\;\vec{c}$$ знайдені, а тому $$\vec{d}=\left \{ -\frac{1}{4};\frac{7}{4};\frac{5}{2} \right \}$$.
Довжиною вектора в координатах називається відстань між точками початку і кінця вектора.
Отже, якщо задано дві точки в просторі, $$A(x_{A};y_{A};z_{A})$$ (початок) і $$B(x_{B};y_{B};z_{B})$$ (кінець вектора), то $$\left |\overrightarrow{AB} \right |=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2+(z_{B}-z_{A})^2}$$.
Якщо точка $$M(x;y;z)$$ ділить відрізок $$AB$$ у співвідношенні $$\lambda$$, то координати цієї точки визначаються так:
$$x=\frac{x_{A}+\lambda x_{B}}{1+\lambda},\;y=\frac{y_{A}+\lambda y_{B}}{1+\lambda},\;z=\frac{z_{A}+\lambda z_{B}}{1+\lambda}.$$
Зокрема, якщо точка $$M(x;y;z)$$ співпадає з серединою відрізка $$AB$$, то
$$x=\frac{x_{A}+x_{B}}{2},\;y=\frac{y_{A}+y_{B}}{2},\;z=\frac{z_{A}+z_{B}}{2}.$$