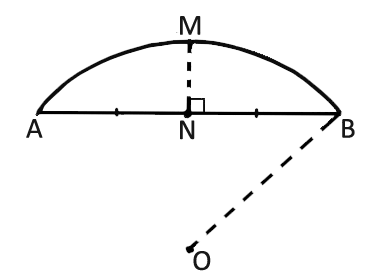
На рисунке схематично изображен выпуклый мост, имеющий форму дуги $$AMB$$ окружности с центром в точке $$O.$$ $$MN$$ – серединный перпендикуляр к $$AB,$$ $$MN=3$$ м. Определить длину радиуса $$OB$$ (в метрах), если длина отрезка $$AB$$ равна 12 м.
Решение
Рассмотрим треугольник $$\triangle ONB: \angle N=90^{\circ}$$
По теореме Пифагора $$OB^2=ON^2+NB^2$$
Пусть $$OM=OB=x$$ – радиус окружности. Тогда $$ON=OM-MN=x-3,$$ $$NB=\frac{1}{2}AB=6$$
$$x^2=(x-3)^2+36$$
$$x^2=x^2+9-6x+36$$
$$6x=45$$
$$x=7.5$$
Ответ: $$7.5$$