Задание 1
Знайдіть натуральне, одноцифрове число N, якщо відомо, що сума 510+N ділиться на 9 без остачі.
| А | Б | В | Г | Д |
| 1 | 3 | 5 | 6 | 9 |
Решение:
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Число N одноцифровое (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
Найдем сумму цифр числа 510+N=5+1+N=6+N
Очевидно, что искомое число N=3, т.к. 6+3=9 делится на 9
Ответ: Б.
Задание 2
Визначте кількість усіх дробів із знаменником 28, які більші за $$\frac{4}{7},$$ але менші від $$\frac{3}{4}.$$
| А | Б | В | Г | Д |
| шість | чотири | три | два | один |
Решение:
$$\frac{4}{7}=\frac{16}{28}<\frac{x}{28}<\frac{3}{4}=\frac{21}{28}$$
$$\frac{17}{28};\frac{18}{28};\frac{19}{28};\frac{20}{28}$$ – четыре искомые дроби.
Ответ: Б
Задание 3
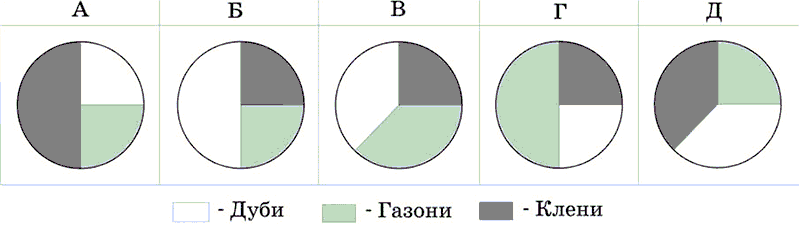
Під час закладання нового парку 25% його площі відвели під посадку кленів, 50% площі, що залишилася, ⎯ під посадку дубів, а решту площі ⎯ під газони. Вкажіть, на якій із діаграм правильно показано розподіл посадок.
Решение:
Под посадку кленов отвели 25% всей площади – это $$\frac{1}{4}$$ (либо Б, либо В, либо Г).
Значит осталось 75% от всей площади, т.е. $$\frac{3}{4}.$$
По условию 50% от оставшейся площади (от $$\frac{3}{4})$$ отвели под дубы. Значит нам нужно распределить поровну оставшуюся часть для дубов и газонов $$(\frac{3}{4}\cdot\frac{1}{2}=\frac{3}{8}$$ от всей площади). Такому распределению соответствует лишь В.
Ответ: В
Задание 4
Розв’яжіть нерівність $$\frac{x^2+64}{x-5}>0.$$
| А | Б | В | Г | Д |
| $$(-\infty;5)\cup (8;\infty)$$ | $$(-\infty;5)\cup (5;\infty)$$ | $$(5;8)$$ | $$(5;\infty)$$ | $$(-\infty;5)$$ |
Решение:
$$x^2+64>0$$ $$\Rightarrow x-5>0$$ $$\Rightarrow x>5$$
Ответ: Г
Задание 5
Якщо $$F=\frac{GMm}{R^2}$$ і $$R>0,$$ то $$R=$$
| А | Б | В | Г | Д |
| $$\sqrt{FGMm}$$ | $$\sqrt{\frac{Mm}{GF}}$$ | $$\sqrt{\frac{GF}{Mm}}$$ | $$\sqrt{\frac{F}{GMm}}$$ | $$\sqrt{\frac{GMm}{F}}$$ |
Решение:
$$F=\frac{GMm}{R^2}$$ $$\Rightarrow R^2=\frac{GMm}{F}$$ $$\Rightarrow R=\sqrt{\frac{GMm}{F}}$$
Ответ: Д
Задание 6
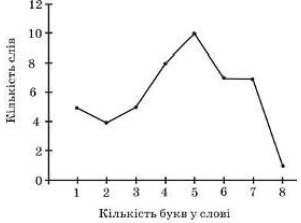
В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода − це те значення випадкової величини, яке зустрічається найчастіше) даного розподілу за допомогою зображеного на рисунку полігона частот.
| А | Б | В | Г | Д |
| 2 | 4 | 5 | 8 | 10 |
Решение:
Из полигона частот, изображенного на рисунке, видно, что чаще всего встречаются слова (10 слов), состоящие из пяти букв, значит мода равна 5.
Ответ: В