Задание 19
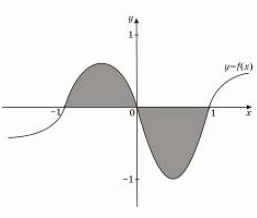
На рисунку зображено графік функції $$y=f(x)$$. Укажіть формулу для обчислення площі зафарбованої фігури.
| А | Б | В | Г | Д |
| $$\int_{-1}^{1}f(x)dx$$ | $$\int_{-1}^{0}f(x)dx-\int_{0}^{1}f(x)dx$$ | $$\int_{0}^{1}f(x)dx-\int_{-1}^{0}f(x)dx$$ | $$2\int_{-1}^{0}f(x)dx$$ | $$2\int_{0}^{1}f(x)dx$$ |
Решение:
$$\int_{-1}^{0}(f(x)-0)dx+\int_{0}^{1}(0-f(x))dx=\int_{-1}^{0}f(x)dx-\int_{0}^{1}f(x)dx$$
Ответ: Б.
Задание 20
Знайдіть значення виразу $$\frac{\sqrt{9+a^2-6a}}{a-3}$$, якщо $$a=2.5.$$
| А | Б | В | Г | Д |
| -1 | -0.5 | 0 | 0.5 | 1 |
Решение:
$$\frac{\sqrt{9+a^2-6a}}{a-3}=\frac{\sqrt{(3-a)^2}}{a-3}=\frac{|3-a|}{a-3}=\left \{ a=2.5 \right \}=\frac{3-a}{a-3}=-1$$
Ответ: А.
Задание 21
Тіло рухається прямолінійно за законом $$s(t)=\frac{2}{3}t^3-2t^2+4t$$ (час $$t$$ вимірюється в секундах, шлях $$s$$ – в метрах). Визначте прискорення його руху в момент $$t=10$$ с.
| А | Б | В | Г | Д |
| 164 м/с2 | 60 м/с2 | 36 м/с2 | 20 м/с2 | 10 м/с2 |
Решение:
Найдем ускорение, т.е. производную.
$${s}'(t)=2t^2-4t+4$$
$$s^{\prime\prime}(t)=4t-4$$
Найдем ускорение движения в момент времени $$t=10$$ с
$$s^{\prime\prime}(10)=4\cdot10-4=40-4=36$$ м/с2
Ответ: В.
Задание 22
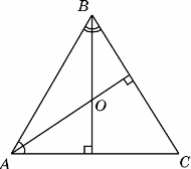
У трикутнику $$ABC$$ $$\angle A=59^{\circ}, \angle B=62^{\circ}$$. Із вершин цих кутів проведено висоти, що перетинаються в точці $$O$$. Визначте величину кута $$AOB$$.
| А | Б | В | Г | Д |
| $$98^{\circ}$$ | $$121^{\circ}$$ | $$144^{\circ}$$ | $$149^{\circ}$$ | $$154^{\circ}$$ |
Решение:
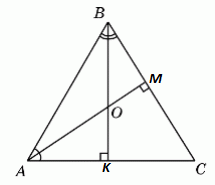
Рассмотрим треугольники:
$$ABK: \angle K=90^{\circ},\angle A=59^{\circ}\Rightarrow \angle ABK=90^{\circ}-59^{\circ}=31^{\circ}$$
$$ABM: \angle M=90^{\circ},\angle B=62^{\circ}\Rightarrow \angle BAM=90^{\circ}-62^{\circ}=28^{\circ}$$
$$AOB: \angle A=28^{\circ},\angle B=31^{\circ}\Rightarrow \angle O=180^{\circ}-28^{\circ}-31^{\circ}=121^{\circ}$$
Ответ: Б.
Задание 23
Сторони трикутника, одна з яких на 8 см більша за другу, утворюють кут $$120^{\circ}$$, а довжина третьої сторони дорівнює 28 см. Знайдіть периметр трикутника.
| А | Б | В | Г | Д |
| 84 см | 72 см | 64 см | 60 см | 56 см |
Решение:
Пусть одна сторона треугольника равна $$a$$, вторая – $$a+8$$ и третья – $$28$$. По теореме косинусов:
$$28^2=a^2+(a+8)^2-2a(a+8)\cos 120^\circ$$
$$784=a^2+a^2+64+16a-2a(a+8)\left (-\frac{1}{2} \right )$$
$$3a^2+24a-720=0$$
$$a^2+8a-240=0$$
По теореме Виета: $$a_{1}+a_{2}=-8, a_{1}\cdot a_{2}=-240$$
$$a_{1}=12$$ – корень
$$a_{2}=-20$$ – посторонний корень
$$P=a+(a+8)+28=12+20+28=60$$
Ответ: Г.
Задание 24

На рисунку зображено розгортку поверхні тіла, складеного з двох квадратів і чотирьох однакових прямокутників, довжина сторін яких ─ 3 см і 6 см. Визначте об’єм цього тіла.
| А | Б | В | Г | Д |
| 108 см3 | 54 см3 | 144 см3 | 36 см3 | Інша відповідь |
Решение:
$$V=abc, a=b=6, c=3\Rightarrow V=6^2\cdot3=108$$
Ответ: А.