ЗНО — 2012 з математики. 1 сесія. Онлайн тест

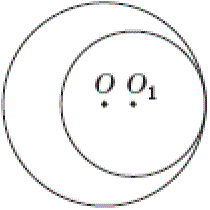
Два кола з центрами в точках $$O$$ і $$O_1$$ мають внутрішній дотик (див. рисунок). Обчисліть відстань $$OO_1,$$  якщо радіуси кіл дорівнюють 12 см і 8 см.

Знайдіть область визначення функції $$y=2-\frac{1}{x}.$$

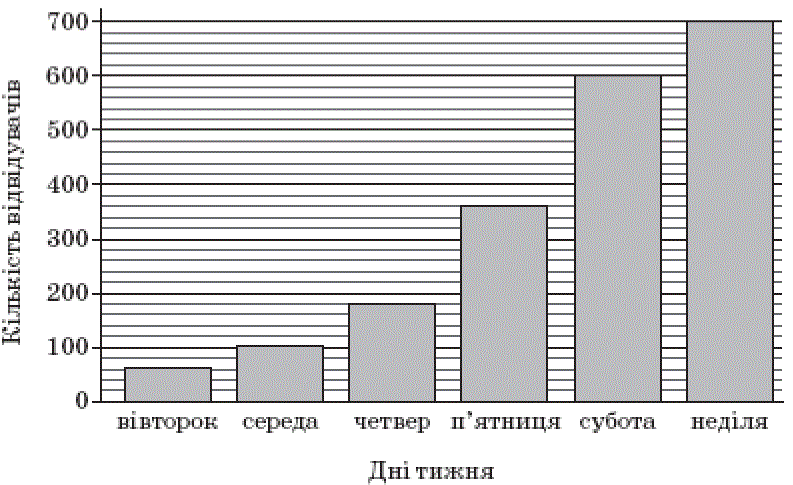
На діаграмі відображено кількість відвідувачів Музею Води протягом одного робочого тижня (з вівторка до неділі). У який день тижня кількість відвідувачів була вдвічі більшою, ніж у попередній день?

Яка з наведених точок належить осі $$Oz$$ прямокутної системи координат у просторі?

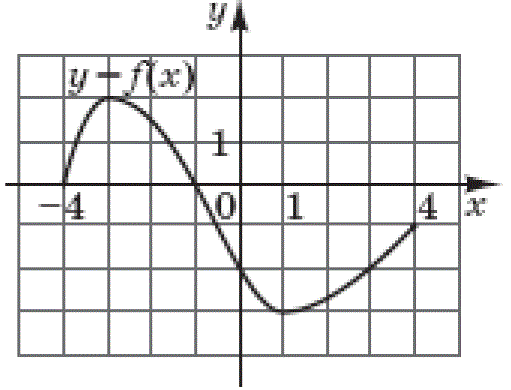
На рисунку зображено графік функції $$y=f(x),$$ визначеної на проміжку $$[-4;4].$$ Знайдіть множину всіх значень $$x,$$ для яких $$f(x)\leq -2.$$

Два фахівці розробили макет рекламного оголошення. За работу вони отримали 5000 грн, розподіливши гроші таким чином: перший отримав четверту частину зароблених грошей, а другий – решту. Скільки гривень отримав за цю роботу другий фахівець?

Пряма $$c$$ перетинає паралельні прямі $$a$$ і $$b$$ (див. рисунок). Які з наведених тверджень є правильними для кутів 1, 2, 3?

Запишіть числа $$\sqrt[3]{2}, 1, \sqrt[5]{3}$$ в порядку зростання.

При якому значенні $$x$$ вектори $$\vec{a}(2;x)$$ і $$\vec{b}(-4;10)$$ перпендикулярні?

На якому з наведених рисунків зображено ескіз графіка функції $$y=4-(x-1)^2?$$

У залі кінотеатру 18 рядів. У першому ряду знаходяться 7 місць, а в кожному наступному ряду на 2 місця більше, ніж у попередньому. Скільки всього місць у залі?

Прямокутник із сторонами 8 см і 10 см обертається навколо меншої сторони (див. рисунок). Знайдіть площу повної поверхні отриманого тіла обертання.

Якому проміжку належить значення виразу $$\sin 410^{\circ}?$$

З міст А і В, відстань між якими по шосе становить 340 км, одночасно назустріч один одному виїхали автобус і маршрутне таксі зі сталими швидкостями 65 км/год відповідно. Автобус і маршрутне таксі рухаються без зупинок і ще не зустрілися. За якою формулою можна обчислити відстань $$S$$ (у км) між автобусом і маршрутним таксі по шосе через $$t$$ годин після початку руху?

Висота правильної чотирикутної піраміди дорівнює 4 см, а її апофема – 5 см. Визначте косинус кута між площиною бічної грані піраміди і площиною основи.

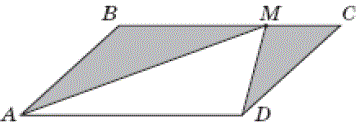
На рисунку зображено паралелограм ABCD, площа якого дорівнює 60 см². Точка М належить стороні BC. Визначте площу фігури, що складається з двох зафарбованих трикутників.

Розв’яжіть нерівність $$(\frac{\pi}{4})^x<(\frac{4}{\pi})^3.$$

У прямокутнику ABCD: BC=80, AC=100. Через точки М і К, що належать сторонам АВ і ВС відповідно, проведено пряму, паралельну АС. Знайдіть довжину більшої сторони трикутника МВК, якщо ВК=20.

Укажіть множину всіх значень $$a,$$ при яких виконується рівність $$|a^3-a^2|=a^3-a^2.$$

Функція $$f(x)$$ має в точці $$x_{0}$$ похідну $$f{}'(x_{0})=-4.$$ Визначте значення похідної функції $$g(x)=2\cdot f(x)+7x-3$$ в точці $$x_{0}.$$

До кожного виразу при $$a>0$$ доберіть тотожно йому рівний.

Кожній точці поставте у відповідність функцію, графіку якої належить ця точка.

Розв’яжіть рівняння. Установіть відповідність між кожним рівнянням та кількістю його коренів на відрізку $$[-5;5].$$

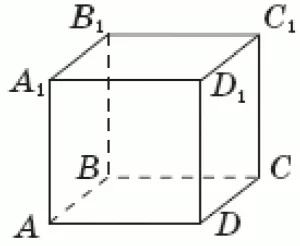
На рисунку зображено куб $$ABCDA_{1}B_{1}C_{1}D_{1}.$$ До кожного початку речення доберіть його закінчення так, щоб утворилося правильне твердження.

Батьки разом із двома дітьми: Марійкою (4 роки) та Богданом (7 років) – збираються провести вихідний день у парку атракціонів. Батьки дозволяють кожній дитині відвідати не більше троьх атракціонів і кожний атракціон – лише по одному разу. Відомо, що на атракціони “Електричні машинки” і “Веселі гірки” допускають лише дітей старше 6 років. На “Паравозик” Богдан не піде. Для відвідування будь-якого атракціону необхідно купити квиток для кожної дитини. Скористувавшись таблицею, визначте максимальну суму коштів (у грн), що витратять батьки на придбання квитків для дітей.

Скільки існує різних дробів $$\frac{a}{b},$$ якщо $$a$$ набуває значень 1; 2 або 4, а $$b$$ набуває значень 5; 7; 11; 13 або 17?

Розв’яжіть систему рівнянь $$\left\{\begin{matrix} y-x=9\\ \frac{x+8}{2y-5}=2 \end{matrix}\right..$$ Запишіть у відповідь добуток $$x_{0}\cdot y_{0},$$ якщо пара $$(x_{0}; y_{0})$$ є розв’язком цієї системи рівнянь.

Обчисліть значення виразу $$\log_{a}500-\log_{a}4,$$ якщо $$\log_{5}a=\frac{1}{4}.$$

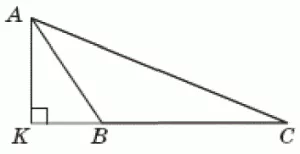
У трикутнику $$\triangle ABC$$ основа висоти $$AK$$ лежить на продовженні сторони $$BC$$ (див. рисунок). $$AK=6,KB=2\sqrt{3}.$$ Радіус описаного навколо трикутника $$\triangle ABC$$ кола дорівнює $$15\sqrt{3}.$$ Визначте довжину $$AC.$$

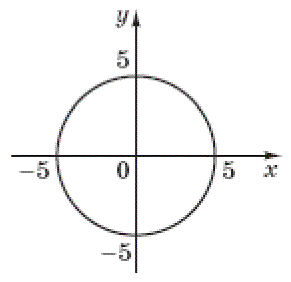
Обчисліть $$\frac{1}{\pi}\int_{-5}^{0}\sqrt{25-x^2}dx,$$ використовуючи рівняння кола $$x^2+y^2=25,$$ зображеного на рисунку.

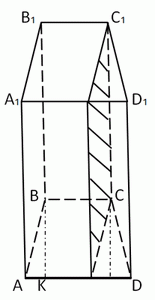
Основою прямої призми $$ABCDA_{1}B_{1}C_{1}D_{1}$$ є рівнобічна трапеція $$ABCD.$$ Основа $$AD$$ трапеції дорівнює висоті трапеції і в шість разів більша за основу $$BC.$$ Через бічне ребро $$CC_{1}$$ призми проведено площину паралельно ребру $$AB.$$ Знайдіть площу утвореного перерізу (у см²), якщо об’єм призми дорівнює 672 см³, а її висота – 8 см.

При якому найменшому цілому значенні параметра $$a$$ рівняння

$$\sqrt{2x+15}\cdot (\sqrt{x^2+18x+81}-\sqrt{x^2-10x+25})=a\sqrt{2x+15}$$

має лише два різні корені?