Найти наибольшее значение функции $$y=\frac{(1-2\cos x)^4}{2}.$$
Решение
Используем свойства косинусоиды. Областью значений косинуса является отрезок [ −1; 1].
$$-1\leqslant\cos x\leqslant 1$$
Умножим двойное неравенство на $$-2<0,$$ изменив при этом знаки неравенства на противоположные. Запишем двойное неравенство в привычном виде (меньшее слева, большее справа).
$$-2\leqslant -2\cos x\leqslant 2$$
Прибавим 1
$$-1\leqslant 1-2\cos x\leqslant 3$$
Перед возведением в четвертую степень вспомним следующие утверждения:
Первое
Неравенства $$f (x) > g (x)$$ и $$(f (x))^{2m}> (g (x))^{2m},$$ где $$m\in\mathbb{N},$$ равносильны на том множестве $$M,$$ где $$f(x)\geqslant 0$$ и $$g(x) \geqslant 0.$$
Второе
Неравенство, обе части которого положительны, можно возвести в любую натуральную степень.
Возведем в 4-ю степень
$$0\leqslant (1-2\cos x)^4\leqslant 81$$
Разделим на $$2>0,$$ оставив при этом знаки неравенства неизменными
$$0\leqslant \frac{(1-2\cos x)^4}{2}\leqslant 40.5$$
Следовательно, наибольшее значение функции $$y$$ равно $$40.5.$$
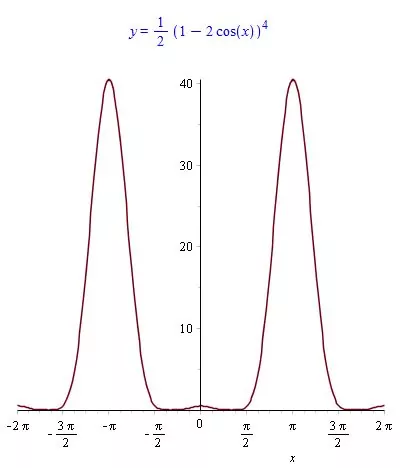
$$y=\frac{(1-2\cos x)^4}{2}.$$
Ответ: $$40.5.$$