В основании пирамиды ромб, тупой угол которого равен $$120^{\circ}.$$ Две боковые грани пирамиды, содержащие стороны этого угла, перпендикулярны к плоскости основания, а две другие боковые грани наклонены к плоскости основания под углом $$30^{\circ}.$$ Найти площадь боковой поверхности пирамиды (в см2), если ее высота равна 4 см.
Решение
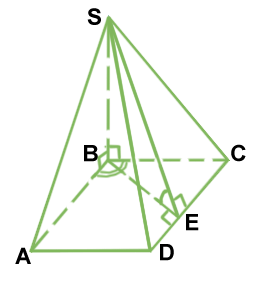
$$SABCD$$ – пирамида. $$ABCD$$ – ромб: $$\angle ABC=\angle ADC=120^{\circ},$$ $$\angle BAD = \angle BCD=180^{\circ}-120^{\circ}=60^{\circ},$$ $$BE \perp DC,$$ $$BE$$ – высота ромба. $$(SBA)\perp (ABCD),$$ $$(SBC)\perp (ABCD),$$ т.е. $$SB=5$$ см – высота пирамиды. $$\angle SEB=30^{\circ}$$
$$\triangle SBA=\triangle SBC$$ (по двум сторонам: $$SB$$ – общая, $$AB=BC$$ и углу между ними: $$\angle SBA=\angle SBC =90^{\circ}$$), значит $$SA=SC$$ и $$S_{\triangle SBA}=S_{\triangle SBC}.$$
$$\triangle SDA=\triangle SDC$$ (по трем сторонам $$SD$$ – общая, $$AD=DC,$$ $$SA=SC$$), значит $$S_{\triangle SDA}=S_{\triangle SDC}.$$
Тогда площадь боковой поверхности пирамиды можно найти по формуле:
$$S=S_{\triangle SBA}+S_{\triangle SBC}+S_{\triangle SDA}+S_{\triangle SDC}=2(S_{\triangle SBC}+S_{\triangle SDC})$$
Площади треугольников можно найти по формулам: $$S_{\triangle SBC}=\frac{1}{2}BC\cdot SB$$ и $$S_{\triangle SDC}=\frac{1}{2}DC\cdot SE.$$
Значит $$S=2(\frac{1}{2}BC\cdot SB+\frac{1}{2}DC\cdot SE)=BC\cdot SB+BC\cdot SE=BC(SB+SE)$$
Рассмотрим $$\triangle SBE:$$ $$\angle B=90^{\circ},$$ $$\angle E=30^{\circ},$$ $$SB=5$$ см – катет против угла в $$30^{\circ}$$ и он равен половине гипотенузы $$SE,$$ значит $$SE=10$$ см. По теореме Пифагора $$BE=\sqrt{10^2-5^2}=\sqrt{(10-5)(10+5)}=\sqrt{5\cdot15}=\sqrt{5^2\cdot3}=5\sqrt{3}$$ см.
$$BE$$ – высота ромба и высота равностороннего треугольника $$BCD$$ (углы по $$60^{\circ}$$) может быть вычислена по формуле $$h=\frac{\sqrt{3}}{2}a,$$ где $$a$$ – сторона равностороннего треугольника (она же является и стороной ромба).
Значит, с одной стороны $$BE=5\sqrt{3}$$ см, а с другой – $$BE=\frac{\sqrt{3}}{2}a.$$ Приравняем и найдем сторону ромба: $$a=\frac{5\sqrt{3}\cdot2}{\sqrt{3}}=10$$ см.
Тогда $$S=10(5+10)=150$$ см2.
Ответ: 150.