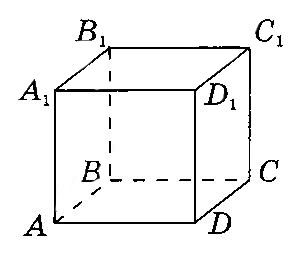
На рисунке изображен куб $$ABCDA_1B_1C_1D_1,$$ ребро которого равно 1 см. Вычислить расстояние от точки $$A$$ до прямой $$B_1C_1.$$
А. 1 см
Б. 2 см
В. $$\sqrt{2}$$ см
Г. 3 см
Д. 1.5 см
Решение
Проведем диагональ $$AB_1\perp B_1C_1$$ – расстояние от точки $$A$$ до прямой $$B_1C_1.$$
Из прямоугольного треугольника $$ABB_1: \angle B=90^{\circ}$$ по теореме Пифагора $$AB_1=\sqrt{AB^2+BB_1^2}=\sqrt{2}$$ (использовали условие, что ребро куба равно 1 см)
Ответ: В