Задание 7
Укажіть правильну нерівність, якщо $$a=5\sqrt{2}, b=7, c=\sqrt{51}$$
| А | Б | В | Г | Д |
| $$b<a<c$$ | $$a<b<c$$ | $$c<a<b$$ | $$a<c<b$$ | $$b<c<a$$ |
Решение:
$$a=5\sqrt{2}=\sqrt{50}, b=7=\sqrt{49}, c=\sqrt{51}$$
$$49<50<51\Rightarrow \sqrt{49}<\sqrt{50}<\sqrt{51}\Rightarrow b<a<c$$
Ответ: А.
Задание 8
Знайдіть значення виразу $$\cos^4\frac{\pi}{12}-\sin^4\frac{\pi}{12}$$
| А | Б | В | Г | Д |
| $$1$$ | $$\frac{\sqrt{3}}{2}$$ | $$\frac{1}{2}$$ | $$\frac{\sqrt{2}}{2}$$ | інша відповідь |
Решение:
$$\cos^4\frac{\pi}{12}-\sin^4\frac{\pi}{12}=(\cos^2\frac{\pi}{12}-\sin^2\frac{\pi}{12})(\cos^2\frac{\pi}{12}+\sin^2\frac{\pi}{12})=\cos \frac{\pi}{6}\cdot1=\frac{\sqrt{3}}{2}$$
Ответ: Б.
Задание 9
Знайдіть найменший додатний період функції $$y=2\cdot ctg 3x$$
| А | Б | В | Г | Д |
| $$2\pi$$ | $$\pi$$ | $$\frac{\pi}{3}$$ | $$\frac{2\pi}{3}$$ | $$\frac{\pi}{2}$$ |
Решение:
$$ctg(x+k\pi)=ctg x, k\in \mathbb{Z}, \pi$$ – наименьший положительный период функции $$ctg x$$.
$$ctg 3x=ctg(3x+k\pi)=ctg 3(x+\frac{k\pi}{3}), k\in \mathbb{Z}, \frac{\pi}{3}$$ – наименьший положительный период функции $$y=2\cdot ctg 3x$$.
Ответ: В.
Задание 10
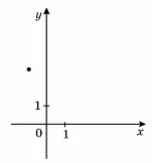
На рисунку зображено точку, через яку проходить графік функції $$y=f(x)$$. Укажіть функцію $$f(x)$$.
| А | Б | В | Г | Д |
| $$f(x)=-x$$ | $$f(x)=\sqrt{x}$$ | $$f(x)=\log_{2}x$$ | $$f(x)=x^3$$ | $$f(x)=3^{-x}$$ |
Решение:
Из графика видно, что точка лежит во II полуплоскости, т.е. $$x$$ принимает отрицательное значение, а $$y$$ – положительное. $$f(x)=\sqrt{x}$$, $$f(x)=\log_{2}x$$ не подходят, т.к. для данных функций $$x$$ не может быть отрицательным. $$f(x)=x^3$$ не подходит, т.к. данная функция является нечетной и отрицательному значению переменной должно соответствовать отрицательное значение функции. $$f(x)=-x$$ не подходит, т.к. функция должна принимать значение переменной с противоположным знаком (из графика видно, что значение функции в несколько раз больше). Остается функция $$f(x)=3^{-x}=\frac{1}{3^x}=\left (\frac{1}{3} \right )^x$$ – убывающая функция (показательная функция с основанием между нулем и единицей), которая и является ответом (например, $$x=-1\Rightarrow y=3$$).
Ответ: Д.
Задание 11
Розв’яжіть рівняння $$\sin x-\sqrt{3}\cos x=0$$
| А | Б | В | Г | Д |
| $$-\frac{\pi}{6}+\pi n, n\in \mathbb{Z}$$ | $$-\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$ | $$\frac{\pi}{6}+\pi n, n\in \mathbb{Z}$$ | $$\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$ | $$\frac{\pi}{2}+\pi n, n\in \mathbb{Z}$$ |
Решение:
Вспомним формулу:
$$a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\phi), tg\phi=\frac{b}{a}$$
В нашем случае:
$$a=1, b=-\sqrt{3}\Rightarrow \sin x-\sqrt{3}\cos x=\sqrt{1^2+(-\sqrt{3})^2}\sin(x+\phi)$$
$$tg\phi=-\sqrt{3}\Rightarrow \phi=arctg(-\sqrt{3})=-\frac{\pi}{3}$$
Значит $$\sin x-\sqrt{3}\cos x=2\sin(x-\frac{\pi}{3})$$
Получили уравнение:
$$2\sin(x-\frac{\pi}{3})=0$$
$$\sin(x-\frac{\pi}{3})=0$$
Вспомним формулу (частный случай):
$$\sin x=0\Rightarrow x=\pi n, n\in \mathbb{Z}$$
В нашем случае:
$$x-\frac{\pi}{3}=\pi n, n\in \mathbb{Z}\Rightarrow x=\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$
Ответ: Г.
Задание 12
Обчисліть $$\log_{a}\sqrt{ab}$$, якщо $$\log_{a}b=7$$
| А | Б | В | Г | Д |
| $$\frac{2}{3}$$ | $$2$$ | $$3$$ | $$\frac{7}{2}$$ | $$4$$ |
Решение:
$$\log_{a}\sqrt{ab}=\log_{a}\left (ab \right )^\frac{1}{2}=\frac{1}{2}\log_{a}ab=\frac{1}{2}\cdot\left (\log_{a}a+\log_{a}b \right )=\frac{1}{2}\cdot\left ( 1+7 \right )=4$$
Ответ: Д.