Тест “Целые уравнения” с выбором ответа

$$x_1=14, x_2=-20$$
$$x_1\cdot x_2=-280$$

$$x-1=3$$ или $$x-1=-3$$
$$x=4, x=-2$$
$$4+(-2)=2$$

$$D=(-2)^2-4\cdot3\cdot(-5)=64$$
$$D_1=(-1)^2-3\cdot(-5)=16$$

$$x_1+x_2=\frac{5}{2}$$

$$x_1+x_2=\sqrt{2}+\sqrt{8}=\sqrt{2}+2\sqrt{2}=3\sqrt{2}$$
$$x_1\cdot x_2=\sqrt{2}\cdot\sqrt{8}=\sqrt{16}=4$$
$$x^2-3\sqrt{2}x+4=0$$

$$10x^2+7x-12=0$$
$$D=23^2$$
$$x_1=-\frac{3}{2}=-1.5$$
$$x_2=0.8$$
$$-1+0=-1$$

$$y=|x^2-3x+2|$$ – график расположен в верхней полуплоскости
$$y=2$$ – прямая, проходящая через $$y=2$$ и параллельная оси $$Ox$$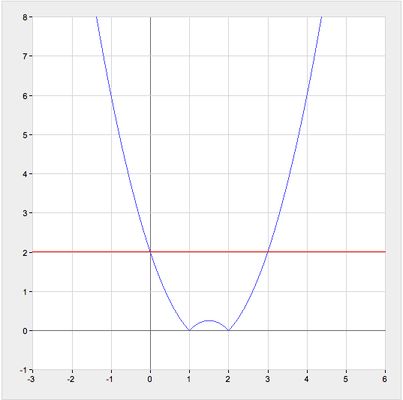

Очевидно, что данные функции пересекаются в 2-х точках, значит уравнение имеет 2 корня.

$$0\cdot x= 0$$ – бесконечное множество решений
$$a^2-1=0$$ и $$a^2+5a-6=0$$
$$a=\pm1$$ и $$a=1, a=-6$$
Общий корень $$a=1$$

$$(a^2-49)x=2a(a+7)$$
$$(a-7)(a+7)x-2a(a+7)=0$$
$$(a+7)[(a-7)x-2a]=0$$
При $$a=-7$$ множество решений,
При $$a=7$$ решений нет
При $$a\neq\pm7$$ единственное решение $$x=\frac{2a}{a-7}$$

$$|-4(2-x)|+|2-x|=4$$
$$4|2-x|+|2-x|=4$$
$$5|2-x|=4$$
$$|2-x|=0.8$$
$$2-x=0.8$$ или $$x-2=0.8$$
$$x=1.2$$ или $$x=2.8$$
$$1.2+2.8=4$$

$$x_1+x_2=3$$
$$x_1\cdot x_2=-5$$
$$(x_1+x_2)^2=x_1^2+x_2^2+2x_1\cdot x_2$$
$$x_1^2+x_2^2=3^2-2\cdot(-5)$$
$$x_1^2+x_2^2=19$$

$$|x|=t\geqslant0$$
$$t^2-7t+10=0$$
$$t_1=2; t_2=5$$
$$x=\pm2; x=\pm5$$