Несколько основных способов решения уравнений с модулем
Предлагаем вспомнить определение модуля и его основные свойства
Рассмотрим основные способы решения уравнений с модулем на примерах.
По определению модуля
$$|2-x|=2x-10$$
Определение модуля: $$|a|=\begin{cases} a, a\geqslant 0\\ -a, a\leqslant 0 \end{cases}$$
$$\left[\begin{matrix} 2-x=2x-10 ,& 2-x\geqslant 0\\ x-2=2x-10, & 2-x2 \end{matrix}\right.$$
$$\left[\begin{matrix} x=4 ,& x\leqslant 2\\ x=8, & x>2 \end{matrix}\right.$$
Очевидно, что $$x=4$$ – посторонний корень, так как $$4>2$$ и не удовлетворяет $$x\leqslant 2.$$
Таким образом, решением исходного уравнения будет $$x=8$$
Ответ: 8.
Возведение в квадрат
$$|2-x|=2x-10$$
Возведем в квадрат обе части уравнения
$$|2-x|^2=(2x-10)^2$$
$$(2-x)^2=(2x-10)^2$$
$$4+x^2-4x=4x^2+100-40x$$
$$3x^2-36x+96=0$$
$$x^2-12x+32=0$$
Получили квадратное уравнение, которое можно решить любым из известных вам способов
$$x_1=4, x_2=8$$
Так как при возведении в квадрат мы могли получить посторонние корни, то необходимо выполнить проверку найденных корней, подстановкой их в исходное уравнение.
Проверкой убеждаемся, что $$x=4$$ – посторонний корень.
Ответ: 8.
Метод интервалов
Данный метод заключается в следующем:
1) определяются нули каждого из модулей, входящего в уравнение (приравниваем нулю выражения под модулем)
2) На числовой прямой отмечаются найденные значения, разбивая при этом прямую на промежутки
3) Решают уравнение на каждом из промежутков
$$|2-x|=2x-10$$
$$2-x=0$$
$$x=2$$
Число 2 разбивает числовую прямую на два промежутка $$(-\infty;2]\cup(2;+\infty)$$
I. Рассмотрим решение при $$x\in(-\infty;2]$$
$$|2-x|=2-x$$
$$2-x=2x-10$$
$$x=4\notin(-\infty;2]$$ – посторонний корень
II. Рассмотрим решение при $$x\in(2;+\infty)$$
$$|2-x|=x-2$$
$$x-2=2x-10$$
$$x=8\in(2;+\infty)$$ – корень уравнения
Ответ: 8.
При решении уравнений рекомендуем учитывать свойства функций и выделять дополнительные условия
$$|2-x|=2x-10$$
Так как модуль является неотрицательной величиной, то и правая часть уравнения должна быть неотрицательной, то есть $$2x-10\geqslant 0.$$ Значит дополнительным условием будет $$x\geqslant 5.$$ При таких значениях $$x$$ выражение под модулем принимает отрицательное значение и модуль раскроется с противоположным знаком.
$$x-2=2x-10$$
$$x=8>5$$ (удовлетворяет дополнительному условию) – корень
Ответ: 8.
Графический способ решения
Графический способ заключается в следующем:
1) Левая и правая части уравнения – две функции от переменной $$x.$$
2) Строятся графики каждой из функций
3) Точки пересечения графиков функций являются искомым решением
$$|2-x|=2x-10$$
$$y=|2-x|=\left[\begin{matrix} 2-x ,& x\leqslant 2\\ x-2, & x>2 \end{matrix}\right.,$$ $$y=2x-10$$
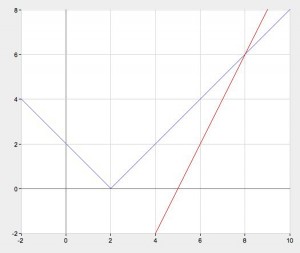
Точкой пересечения графиков данных функций будет точка $$(8;6),$$ то есть $$x=8$$
Ответ: 8.
Графический способ уместен, когда необходимо определить количество корней, не находя их точных значений. Также данный способ довольно часто применяется при решении параметрических уравнений.