Определение
Производной функции $$y=f(x)$$ в точке $$x$$ называется предел отношения приращения функции $$\Delta y$$ к приращению $$\Delta x$$ аргумента $$x,$$ когда приращение аргумента стремится к нулю.
$$y^{\prime}=\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}$$
Основные правила дифференцирования
- Производная от алгебраической суммы функций есть алгебраическая сумма производных: $$\left ( f(x)\pm g(x)\pm h(x) \right )^{\prime}=f'(x)\pm g^{\prime}(x)\pm h^{\prime}(x).$$
- Производная от произведения двух функций есть произведение производной первой функции на вторую функцию плюс произведение первой функции на производную второй функции: $$(u\cdot v)^{\prime}=u^{\prime}\cdot v+u\cdot v^{\prime},\;u=u(x),\;v=v(x).$$
- Постоянное число (константу) можно вынести за знак производной: $$\left ( c f(x) \right )^{\prime}=cf^{\prime}(x),\;c=const.$$
- Производная от частного двух функций есть отношение разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя к знаменателю в квадрате: $$\left ( \frac{u}{v} \right )^{\prime}=\frac{u^{\prime}\cdot v-u\cdot v^{\prime}}{v^2},\;u=u(x),\;v=v(x)\neq0.$$
Таблица производных
| Функция $$y$$ | Производная $$y^{\prime}$$ |
| $$c=const$$ | 0 |
| $$x^n$$ | $$nx^{n-1},\;n\in \mathbb{R}$$ |
| $$a^x$$ | $$a^x\ln a,\;a>0,\;a\neq1$$ |
| $$e^x$$ | $$e^x$$ |
| $$\log_a x$$ | $$\frac{1}{x\ln a},\;a>0,\;a\neq1$$ |
| $$\ln x$$ | $$\frac{1}{x}$$ |
| $$\sin x$$ | $$\cos x$$ |
| $$\cos x$$ | $$-\sin x$$ |
| $$\text{tg}\, x$$ | $$\frac{1}{\cos^2x}$$ |
| $$\text{ctg}\, x$$ | $$-\frac{1}{\sin^2x}$$ |
| $$\arcsin x$$ | $$\frac{1}{\sqrt{1-x^2}}$$ |
| $$\arccos x$$ | $$-\frac{1}{\sqrt{1-x^2}}$$ |
| $$\text{arctg}\, x$$ | $$\frac{1}{1+x^2}$$ |
| $$\text{arcctg}\, x$$ | $$-\frac{1}{1+x^2}$$ |
Геометрический смысл производной
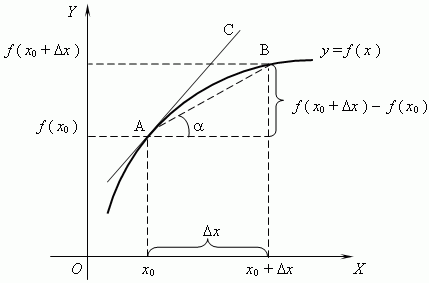
Для любых двух точек $$A(x_0;f(x_0))$$ и $$B(x_0+\Delta x;f(x_0+\Delta x))$$ графика функции $$y=f(x)$$ имеет место $$\text{tg}\,\alpha=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x},$$ где $$\alpha$$ – угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то $$\Delta x$$ неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Производная $$f^{\prime}(x_0)$$ функции $$y=f(x)$$ в точке $$x_0$$ равна угловому коэффициенту (тангенсу угла наклона) касательной к графику функции в этой точке.
Уравнение касательной к графику дифференцируемой функции
$$y-f(x_0)=f^{\prime}(x_0)(x-x_0)$$
Физический смысл производной
Пусть материальная точка движется по координатной прямой, подчиняясь закону $$x=x(t),$$ т.е. координата этой точки $$x$$ – известная функция времени $$t.$$
Физический смысл производной состоит в том, что производная от координаты по времени есть мгновенная скорость: $$v(t)=x^{\prime}_t$$