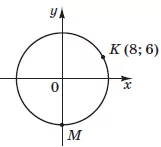
На координатной плоскости $$xy$$ изображена окружность, центр которой совпадает с началом координат (см. рисунок). Точки $$K(8;6)$$ и $$M(x;y)$$ принадлежат этой окружности. Определите координаты точки $$M.$$
А. $$(-10;0)$$
Б. $$(10;0)$$
В. $$(0;-14)$$
Г. $$(0;-10)$$
Д. $$(0;10)$$
Решение:
Один из способов решения данного задания – решение с помощью векторов. Заодно предлагаем вспомнить теорию по данной теме.
Найдем координаты вектора $$\vec{OK}(8-0;6-0)=\vec{OK}(8;6)$$
Длина вектора $$|\vec{OK}|=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$$
Значит радиус окружности равен 10.
Тогда становится очевидным, что координаты точки $$M$$ есть $$x=0$$ (точка на оси $$Oy)$$ и $$y=-10$$ (точка в нижней полуплоскости), т.е. $$M(0;-10).$$
Аналогичного результата можно достичь при рассмотрении прямоугольного треугольника (необходимо опустить перпендикуляр на ос $$Ox)$$ и нахождения по теореме Пифагора гипотенузы, равной радиусу окружности.
Ответ: Г.