Мы уже рассмотрели решения двенадцати тестовых заданий (1-4; 5-8; 9-12) с выбором 1 правильного ответа пробного ЗНО по математике от 30 марта 2013 года, бесплатный онлайн тест которого Вы можете пройти по ссылке: Пробне ЗНО 2013 з математики.
Другие задания ПЗНО: 17-20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32; 33.
Приступим к решению заданий № 13-16.
Задание 13
Спростіть вираз $$\frac{9-x^2}{x^2+6x+9}.$$
А) $$\frac{3-x}{x+3}$$
Б) $$\frac{x-3}{x+3}$$
В) $$3-x$$
Г) $$\frac{1}{x+3}$$
Д) 1
Решение:
Выполним преобразования, применив формулы сокращенного умножения
$$\frac{9-x^2}{x^2+6x+9}=\frac{(3-x)(3+x)}{(x+3)^2}=\frac{3-x}{x+3}$$
Ответ: А.
Задание 14
Діаметр основи конуса дорівнює 6 см, а площа його бічної поверхні – $$24\pi$$ см2. Знайдіть довжину твірної конуса.
А) 2 см
Б) 4 см
В) 6 см
Г) 8 см
Д) 12 см
Решение:
Диаметр основания конуса равен 6 см, значит радиус равен 3 см.
Площадь боковой поверхности конуса находится по формуле
$$S=\pi\cdot R\cdot l$$, где $$R$$ – радиус основания конуса, $$l$$ – образующая конуса. Так как площадь боковой поверхности конуса равна $$24\pi$$ см2, то образующая равна
$$l=\frac{S}{R\pi}=\frac{24\pi}{3\pi}=8$$ см.
Ответ: Г.
Задание 15
На рисунку зображено круг з центром у точці О, радіус якого дорівнює 12 см. Радіуси ОА та ОВ ділять круг на два кругові сектори. Визначте площу більшого сектора, якщо кут $$\alpha=120^{\circ}.$$

А) $$16\pi$$ см2
Б) $$48\pi$$ см2
В) $$96\pi$$ см2
Г) $$108\pi$$ см2
Д) $$144\pi$$ см2
Решение:
Площадь круга находится по формуле
$$S=\pi r^2$$
Площадь меньшего сектора находится по формуле
$$S_1=\frac{\pi r^2\alpha}{360^{\circ}}$$
Площадь большего сектора найдем как разность площади круги и площади меньшего сектора
$$S_2=S-S_1=\pi r^2-\frac{\pi r^2\alpha}{360^{\circ}}=\frac{\pi r^2(360^{\circ}-\alpha)}{360^{\circ}}=$$
$$=\frac{\pi\cdot144\cdot(360^{\circ}-120^{\circ})}{360^{\circ}}=\frac{2}{3}\cdot 144\pi=96\pi$$ см2
Ответ: В.
Задание 16
Апофема правильної чотирикутної піраміди дорівнює 10 см, її висота – 8 см. Знайдіть довжину сторони основи піраміди.
А) 12 см
Б) $$6\sqrt{3}$$ см
В) 4 см
Г) 4 см
Д) $$6\sqrt{2}$$ см
Решение:
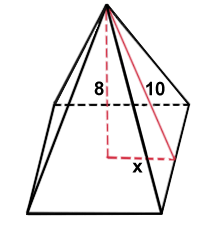
Из прямоугольного треугольника по теореме Пифагора (см. рисунок) найдем $$x$$, который равен половине стороны основания правильной четырехугольной пирамиды
$$x^2=10^2-8^2=100-64=36\Rightarrow x=6$$ см.
Тогда длина стороны равна 12 см.
Ответ: А.