В рамках подготовки к ДПА и ЗНО по математике предлагаем тестовое задание открытого типа, взятое из пробного ЗНО 2013.
Решение других заданий ПЗНО 2013: 1-4; 5-8; 9-12; 13-16; 17-20; 21; 22; 23; 24; 25; 27; 28; 29; 30; 31; 32; 33. Онлайн тест ПЗНО 2013 по математике.
Задание № 26
При якому значенні $$x$$ функція $$y=4-|20x+7|$$ набуває найбільшого значення?
Решение:
Воспользуемся определением модуля и преобразуем функцию
$$y=4-|20x+7|=\left[\begin{matrix} 4-(20x+7), 20x+7\geqslant 0\\ \\ 4-(-20x-7), 20x+7< 0 \end{matrix}\right.=\left[\begin{matrix} -20x-3, x\geqslant -\frac{7}{20}\\ \\ 20x+11, x< -\frac{7}{20} \end{matrix}\right.$$
$$y=20x+11$$ возрастающая функция, а $$y=-20x-3$$ – убывающая.
Значит функция $$y=4-|20x+7|$$ возрастает при $$x\in(-\infty;-\frac{7}{20})$$ и убывает при $$x\in[-\frac{7}{20};\infty)$$, а при $$x=-\frac{7}{20}=-0.35$$ принимает наибольшее значение (см. рисунок).
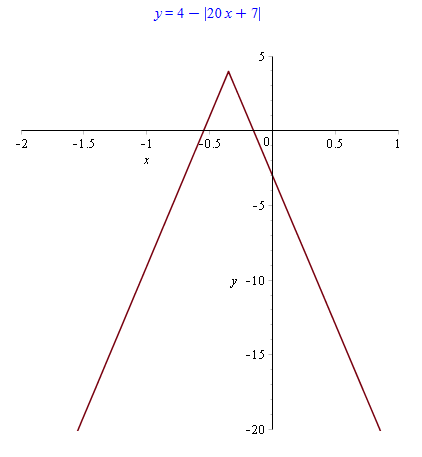
Ответ: $$-0.35$$.