Рассмотрим геометрическую задачу (задание №32 ПЗНО 2013 по математике).
Задание №32
Основою прямої призми $$ABCDA_1B_1C_1D_1$$ є ромб $$ABCD,$$ у якому більша діагональ $$AC=17$$ см. Об’єм призми дорівнює 1020 см3. Через діагональ $$AC$$ та вершину $$B_1$$ тупого кута верхньої основи призми проведено площину, яка утворює з площиною основи кут $$\alpha.$$ Знайдіть площу утвореного перерізу призми (у см2), якщо $$\text{tg}\,\alpha=2.4.$$
Решение:
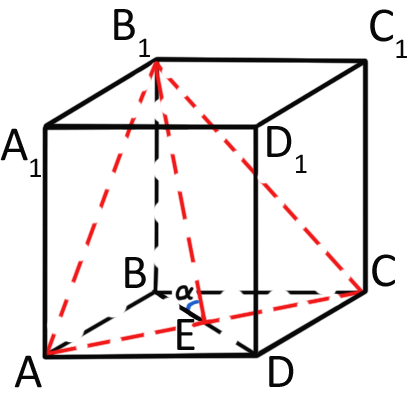
В сечении мы получили треугольник $$AB_1C.$$ Вспомним формулу площади треугольника \(S_{\triangle}= \frac{1}{2}a\cdot h_a.\)
В нашем случае \(a\) – известная диагональ ромба \(AC,\) а \(h_a = B_1E,\) т.е. $$S_{AB_1C}=\frac{1}{2}AC\cdot B_1E.$$
Объем призмы вычисляется по формуле \(V = S\cdot H,\) где \(S \) – площадь основания, \( H\) – высота призмы.
Т.к. призма прямая, то \( H = AA_1=BB_1=CC_1=DD_1.\) По условию основанием призмы является ромб, тогда площадь основания вычисляется по формуле \(S_{ABCD} = \frac{1}{2}AC\cdot BD.\)
Следовательно объем призмы можно найти по формуле $$V =\frac{1}{2}AC\cdot BD \cdot BB_1.$$
$$BB_1$$ найдем из прямоугольного треугольника \( BB_1E:\)
$$BB_1=BE\cdot\text{tg}\alpha,$$ $$\text{tg}\alpha = 2.4,$$ $$BE=\frac{1}{2}BD$$ => $$BB_1 = \frac{1}{2}BD\cdot2.4=1.2\cdot BD.$$
Подставим $$BB_1$$ в формулу объема призмы $$V=\frac{1}{2}AC\cdot BD \cdot1.2\cdot BD=0.6\cdot AC\cdot BD^2.$$
Так как объем призмы равен 1020 см3, $$AC=17$$ см, то $$BD^2=\frac{1020}{0.6\cdot17}=100$$ см2.
Тогда $$BD=10$$ см => $$BE=5$$ см и $$BB_1=12$$ см.
Найдем $$B_1E$$ по теореме Пифагора: $$B_1E=\sqrt{BB_1^2+BE^2}=\sqrt{144+25}=\sqrt{169}=13$$ см.
$$S_{AB_1C}=\frac{1}{2}\cdot17\cdot13=110.5$$ см2.
Ответ: 110.5.
Другие задания ПЗНО 2013: 1-4; 5-8; 9-12; 13-16; 17-20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 33.