Продолжаем решать тестовые задания пробного ЗНО 2013.
Задание №30
У прямокутній трапеції $$ABCD\;(AD\parallel BC)$$ діагональ $$AC$$ перпендикулярна до бічної сторони $$CD.$$ Знайдіть довжину цієї діагоналі (у см), якщо $$AD=18$$ см, $$BC=8$$ см.
Решение:
Из вершины $$C$$ опустим перпендикуляр на основание $$AD$$ (см. рисунок).
Получили $$AB=EC,$$ $$AE=BC=8$$ см, тогда $$ED=AD-AE=18-8=10$$ см.
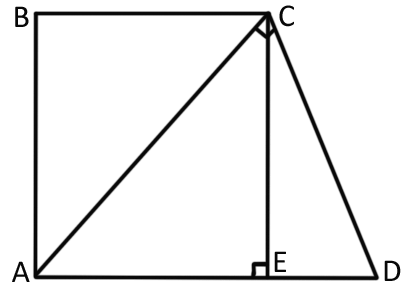
Рассмотрим три прямоугольных треугольника: $$\triangle ACD,$$ $$\triangle CED$$ и $$\triangle AEC.$$
По теореме Пифагора для каждого треугольника получим:
$$\left\{\begin{matrix}AC^2=AD^2-CD^2&(1)\\ CD^2=CE^2+ED^2&(2)\\ CE^2=AC^2-AE^2&(3)\end{matrix}\right.$$
Подставим $$(3)$$ в $$(2),$$ затем полученный результат подставим в $$(1).$$
$$AC^2=AD^2-((AC^2-AE^2)+ED^2)$$
$$AC^2=AD^2-AC^2+AE^2-ED^2$$
$$2AC^2=AD^2+AE^2-ED^2$$
$$AC^2=\frac{1}{2}\cdot(AD^2+AE^2-ED^2)$$
$$AC=\sqrt{\frac{1}{2}\cdot(AD^2+AE^2-ED^2)}$$
Подставим значения. Выполним элементарные преобразования и воспользуемся свойствами корней и степеней.
$$AC=\sqrt{\frac{1}{2}\cdot(18^2+8^2-10^2)}=\sqrt{18\cdot9+8\cdot4-10\cdot5}=\sqrt{18\cdot9+32-50}=\sqrt{18\cdot9-18}=$$
$$=\sqrt{18\cdot(9-1)}=\sqrt{18\cdot8}=\sqrt{3^2\cdot2\cdot2^3}=\sqrt{3^2\cdot4^2}=3\cdot4=12.$$
Длина диагонали $$AC$$ равна 12 см.
Ответ: 12.
Другие задания ПЗНО: 1-4; 5-8; 9-12; 13-16; 17-20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 31; 32; 33.