Задание №29
Обчисліть $$(\sqrt{20})^{2+\log_{20}16}.$$
Решение:
$$(\sqrt{20})^{2+\log_{20}16}=(20)^{\frac{1}{2}\left ( 2+\log_{20}16 \right )}=(20)^{1+\log_{20}4}=20\cdot20^{\log_{20}4}=20\cdot4=80$$
Ответ: 80.
Задание №30
Обчисліть $$\int_{0}^{7}f(x)dx,$$ використовуючи зображений на рисунку графік лінійної функції $$y=f(x).$$
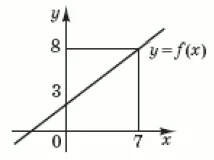
Решение:
Площадь прямоугольника равна $$7\cdot8=56,$$ площадь треугольника равна $$\frac{1}{2}\cdot5\cdot7=17.5.$$ Интеграл равен площади фигуры, которая получается вычитанием площади треугольника от площади прямоугольника: $$\int_{0}^{7}f(x)dx=56-17.5=38.5.$$
Ответ: 38.5
Задание №31
За основою прямої трикутної призми $$ABCA_1B_1C_1$$ є рівнобедрений трикутник $$ABC$$, де $$AB=BC=25$$ см, $$AC=30$$ см. Через бічне ребро $$AA_1$$ призми проведено площину, перпендикулярну до ребра $$BC.$$ Визначте об’єм призми (у см3), якщо площа утвореного перерізу дорівнює 72 см2.
Решение:
$$V=S\cdot H$$ – объем призмы, где $$S$$ – площадь основания призмы (площадь равнобедренного треугольника $$ABC$$), $$H$$ – высота прямой призмы (совпадает с ребром $$AA_1$$).
$$S=\frac{1}{2}\cdot BC\cdot h_{BC}$$ – площадь треугольника $$ABC,$$ где $$h_{BC}$$ – высота треугольника к стороне $$BC.$$
$$S_1=H\cdot h_{BC}$$ – площадь сечения (площадь прямоугольника).
Найдем объем призмы:
$$V=S\cdot H=\frac{1}{2}\cdot BC\cdot h_{BC}\cdot H=\frac{1}{2}\cdot BC\cdot S_1=\frac{1}{2}\cdot 25\cdot 72=900$$
Ответ: 900.
Задание №32
При якому найменшому значенні $$a$$ рівняння
$$\sqrt{x-2+2\sqrt{x-3}}+(14-2a)\cdot\sqrt[4]{x-3}+32=6a$$
має хоча б один корінь?
Решение:
ОДЗ: $$x-3\geqslant 0\Rightarrow x\geqslant 3$$
Выполним преобразования:
$$\sqrt{x-2+2\sqrt{x-3}}=\sqrt{x-3+1+2\cdot\sqrt{x-3}\cdot1}=$$
$$=\sqrt{(\sqrt{x-3})^2+1^2+2\cdot\sqrt{x-3}\cdot1}=\sqrt{(\sqrt{x-3}+1)^2}=|\sqrt{x-3}+1|=$$
$$=\sqrt{x-3}+1$$
Подставим в первоначальное уравнение:
$$\sqrt{x-3}+1+(14-2a)\cdot\sqrt[4]{x-3}+32=6a$$
Сделаем замену:
$$\sqrt[4]{x-3}=t\geqslant 0$$
$$t^2+(14-2a)t+33-6a=0$$
$$t^2+2(7-a)t+33-6a=0$$
Найдем дискриминант для полученного квадратного уравнения:
$$D_1=(7-a)^2-(33-6a)=49+a^2-14a-33+6a=a^2-8a+16=(a-4)^2$$
Уравнение имеет хотя бы 1 корень, если дискриминант неотрицательный. В нашем случае дискриминант равен полному квадрату, который всегда неотрицателен.
1. $$(a-4)^2= 0\Rightarrow a=4$$
$$t=a-7=4-7=-3$$ – посторонний корень
2. $$(a-4)^2> 0\Rightarrow a\neq4$$
$$t_{1,2}=a-7\pm\sqrt{(4-a)^2}=a-7\pm |4-a|$$
$$t_{1,2}=a-7\pm 4\mp a$$ (смотрите опеределение модуля)
$$t=-3$$ – посторонний корень
$$t=2a-11\geqslant 0\Rightarrow a\geqslant 5.5$$
Наименьшее значение параметра $$a = 5.5.$$
Ответ: 5.5