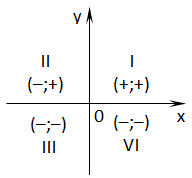Для визначення положення довільної точки використовуються різні системи координат. Положення точки у будь-якій системі координат повинно характеризуватись однозначно. Поняття системи координат являє собою сукупність точки початку відліку (початку координат) і деякого базису. Як на площині, так і в просторі можливе задання доволі різноманітних систем координат. Вибір системи координат залежить від характеру поставленої геометричної, фізичної або технічної задачі. Розглянемо деякі системи координат, які найбільш часто застосовуються на практиці.
Координати точки на прямій та основні задачі
Точку $$M$$ координатної вісі $$OX$$ з абсцисою $$x$$ позначають $$M(x)$$.
Віддаль між двома точками $$M_{1}(x_{1})$$ і $$M_{2}(x_{2})$$ при будь-якому розташуванні їх на осі визначається формулою:
$$d=|x_{2}-x_{1}|$$.
Відрізок $$AB$$ довільної прямої ($$A$$ – початок, $$B$$ – кінець відрізка) може бути поділений за допомогою точки $$C$$ цієї прямої в деякому відношенні $$\lambda$$, яке визначається формулою:
$$\lambda =\pm\frac{AC}{CB}$$.
Знак “+” береться у випадку, коли точка поділу $$C$$ розташована на відрізку $$AB$$ (тоді $$AC$$ і $$CB$$ однаково спрямовані), якщо точка $$C$$ знаходиться поза $$AB$$, то береться знак “–” (тоді відрізки $$AC$$ і $$CB$$ будуть протилежно спрямовані).
Якщо точки $$A$$ і $$B$$ розташовані на осі $$OX$$, а $$C$$ – точка поділу відрізка у відношенні $$\lambda,$$ то координата $$x$$ точки $$C\left (x \right )$$ визначається формулою:
$$x=\frac{x_{1}+\lambda x_{2}}{1+\lambda}.$$
Зокрема, при $$\lambda=1$$ реалізується половинний поділ, тобто $$x=\frac{x_{1}+x_{2}}{2}$$ є координата середини відрізка $$AB$$.
Отже ми розглянули систему координат на прямій, тобто сукупність умов, якими визначається положення точки на прямій, а також дві найпростіші задачі в цій системі.
Декартова прямокутна система координат на площині, найпростіші задачі
Система зветься прямокутною декартовою системою, якщо осі $$OX$$ і $$OY$$ взаємно перпендикулярні і мають одинакові масштабні одиниці.
Якщо спроектуємо точку $$M$$ на осі $$OX$$ і $$OY$$, то $$M$$ має на осі $$OX$$ координату $$x$$ (абсцису), а на осі $$OY$$ координату $$y$$ (ординату).
Знаки координат точок на площині:
Відстань від точки до точки знаходять за формулою:
$$d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}.$$
Якщо відрізок $$AB$$ поділяється точкою $$C$$ у відношенні $$\lambda$$, то координати точки поділу $$C(x,y)$$ через координати точок $$M_{1}(x_{1},y_{1})$$ і $$M_{2}(x_{2},y_{2})$$ виражаються наступним чином:
$$x=\frac{x_{1}+\lambda x_{2}}{1+\lambda},\;y=\frac{y_{1}+\lambda y_{2}}{1+\lambda}.$$
У випадку, коли $$C$$ – середина відрізка $$AB$$, то її координати знаходять так:
$$x=\frac{x_{1}+x_{2}}{2},\;y=\frac{y_{1}+y_{2}}{2}.$$
Площа трикутника з вершинами $$A(x_{A};y_{A}),\;B(x_{B}, y_{B}),\;C(x_{C}, y_{C})$$ визначається за формулою:
$$S=\frac{1}{2}\left | x_{A}\cdot(y_{B}-y_{C})+x_{B}\cdot(y_{C}-y_{A})+x_{C}\cdot(y_{A}-y_{B}) \right |.$$
Полярна система координат. Зв’язок між полярними і декартовими координатами
Положення точки $$M$$ на площині визначається її відстанню $$OM=\rho$$ від полюса $$O$$ ($$\rho$$ – полярний радіус-вектор точки) і кутом $$\phi$$, який утворюється відрізком $$OM$$ з полярною віссю $$OX$$ ($$\phi$$ – полярний кут точки). Кут $$\phi$$ вважається додатним, якщо він збільшується при повороті відрізка $$OM$$ проти годинникової стрілки. Точка $$M(\rho; \phi)$$ має координати $$0\leqslant \rho<\infty,\; 0\leqslant \phi<2\pi.$$
Якщо початок декартової прямокутної системи координат розташувати в полюсі, а вісь $$OX$$ направити вздовж полярної вісі, то прямокутні координати $$x$$ і $$y$$ точки $$M$$ і її полярні координати $$\rho$$ і $$\phi$$ будуть пов’язані наступними формулами:
$$x=\rho\cos\phi,\;\;y=\rho\sin\phi;$$
$$\rho=\sqrt{x^2+y^2},\;\cos\phi=\frac{x}{\sqrt{x^2+y^2}},\;\sin\phi=\frac{y}{\sqrt{x^2+y^2}}.$$