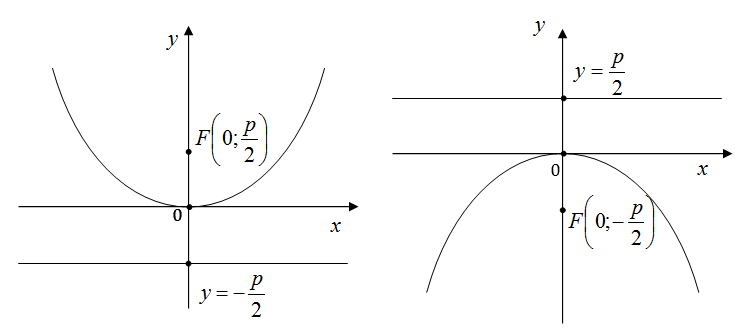Парабола є незамкненою лінією, що складається із однієї гілки.
Аналітично вона є геометричним місцем точок, рівновіддалених від даної точки (фокуса) і від даної прямої (директриси), розташованих в одній площині.
У випадку рівняння $$y^2=2px\;(p>0)$$ парабола симетрична вісі $$OX$$, її вершина співпадає з точкою $$O(0;0)$$, значення параметра $$p$$ чисельно співпадає з віддаллю від фокуса до директриси, рівняння директриси $$x=-\frac{p}{2}$$, координата фокуса $$F\left (\frac{p}{2};0 \right )$$.
У випадку рівняння $$y^2=-2px\;(p>0)$$ парабола має форму
Ця парабола також симетрична відносно вісі $$OX$$.
Існують ще дві параболи, симетричні відносно вісі $$OY$$. Вони мають рівняння
$$x^2=2py\;(p>0)$$ та $$x^2=-2py\;(p>0)$$.