Множина
Множину можна уявити собі як сукупність деяких об’єктів, що об’єднані за якоюсь ознакою. У математиці множини — це одне з основних неозначуваних понять.
Кожний об’єкт, що входить до множини А, називається елементом цієї множини.
Зазвичай елементи позначають малими латинськими літерами: a, b, c, d тощо.
Якщо a належить множині A, то пишуть a ∈ A (читають: «a належить множині A»). Якщо b не належить множині A, то пишуть b ∉ A (читають: «b не належить множині A»).
Множина, що не містить жодного елемента, називається порожньою множиною і позначається ∅.
Дві множини A і B називають рівними, якщо вони складаються з одних і тих самих елементів, тобто кожний елемент множини A належить множині B, і навпаки, кожний елемент множини B належить множині A.
Якщо множини A і B рівні, то пишуть A = B.
З означення випливає, що множина однозначно визначається своїми елементами.
Для ілюстрації співвідношень між множинами використовують схеми, які називають діаграмами (кругами) Ейлера-Венна.
Підмножина
Якщо кожен елемент однієї множини A є елементом другої множини B, то кажуть, що перша множина A є підмножиною другої множини B і записують так: A ⊂ B.
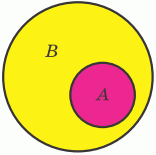
Використовують також запис A ⊆ B, якщо множина A або є підмножиною множини B, або дорівнює множині B.
Операції над множинами
Перетин (переріз) множин
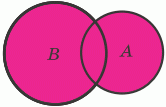
Перетином множин A і B називають множину, яка складається з усіх елементів, що належать і множині A, і множині B. Перетин множин A і B позначають так: $$A\cap B.$$

Об’єднання множин
Об’єднанням множин A і B називають множину, яка складається з усіх елементів, що належать хоча б одній з цих множин: або множині A, або множині B. Об’єднання множин A і B позначають так: $$A\cup B.$$
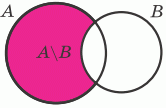
Різниця множин
Різницею множин А і В називається множина, яка складається з усіх елементів, які належать множині А і не належать множині В. Різницю A і B позначають так: $$A\setminus B.$$
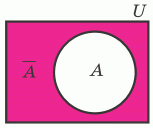
Доповнення множини
Якщо всі множини, які ми розглядаємо, є підмножинами якоїсь так званої універсальної множини U, то різниця U \ A називається доповненням множини A. Тобто доповненням множини A називається множина, яка складається з усіх елементів, які не належать множині А (але які належать універсальній множині U). Доповнення множини A позначають так: $$\overline{A}.$$