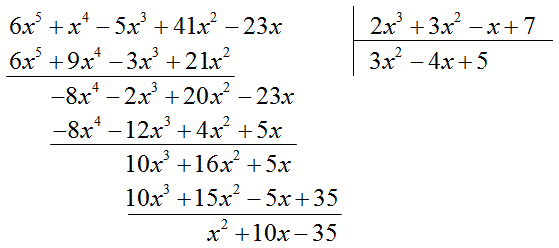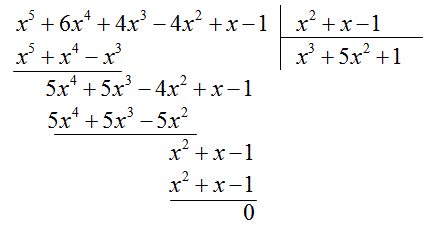Одночленом (мономом) называется выражение вида $$A \cdot x^{\alpha} \cdot y^{\beta} \cdot z^{\gamma}\cdot\ldots$$,
где $$\alpha,\beta,\gamma,\ldots\in\mathbb{Z}_{+},\alpha+\beta+\gamma+\ldots$$ — степень одночлена.
Т.е. одночленом называется рациональное выражение, содержащее относительно входящих в него букв только два действия: умножение и возведение в целую положительную степень. Одночленом также считается любая константа (каждое отдельное число), причём степень такого одночлена равна нулю.
Многочленом (полиномом) называется алгебраическая сумма нескольких одночленов.
$$P(x)=P_{n}(x)=\sum_{i=0}^{n}a_{i}x^i=a_{0}+a_{1}x+a_{2}x^2+\ldots+a_{n}x^n,\;a_{n}\neq0,\;n\in\mathbb{Z}_{+}$$ – многочлен n-й степени, упорядоченный по возрастающим степеням.
$$P_{n}(x)=a_{n}x^n+a_{n-1}x^{n-1}+\ldots+a_{1}x+a_{0},\;a_{n}\neq0,\;n\in\mathbb{Z}_{+}$$ – многочлен n-й степени, упорядоченный по убывающим степеням.
$$x_0$$ называется корнем многочлена $$P(x),$$ если $$P(x_{0})=0.$$
Если одночлены равны или отличаются только коэффициентами, то они называются подобными. Замена алгебраической суммы подобных членов одним, тождественно равным этой сумме, называется приведением подобных членов.
Деление многочленов:
- Упорядочить многочлены по степеням (одинаковое упорядочивание).
- Делим первый член делимого на первый член делителя и получаем первый член частного.
- Умножаем делитель на полученный член частного. Данное произведение вычитаем из делимого и получаем остаток.
- Если остаток равен нулю, то деление окончено. Если не равен, то делим первый член остатка на первый член делителя и получаем следующий член частного. Умножаем на него делитель и вычитаем полученное произведение из остатка.
- Повторяем пункт 4 до тех пор, пока в остатке не получим нуль (деление нацело) или пока первый член очередного остатка не будет делиться на первый член делителя (деление с остатком)
Пример:
$$\frac{-23x+6x^5-5x^3+41x^2+x^4}{2x^3+7-x+3x^2}=?$$
$$\frac{6x^5+x^4-5x^3+41x^2-23x}{2x^3+3x^2-x+7}=3x^2-4x+5+\frac{x^2+10x-35}{2x^3+3x^2-x+7}$$ – деление с остатком.
$$\frac{x^5+6x^4+4x^3-4x^2+x-1}{x^2+x-1}=?$$
$$\frac{x^5+6x^4+4x^3-4x^2+x-1}{x^2+x-1}=x^3+5x^2+1$$ – деление нацело.
Теорема Безу: Остаток от деления многочлена $$P(x)$$ на двучлен $$(x-a)$$ равен $$P(a).$$
Следствия:
- Число $$a$$ является корнем $$P(x)$$ тогда и только тогда, когда $$P(x)$$ делится нацело на двучлен $$(x-a).$$
- Целыми корнями многочлена с целыми коэффициентами могут быть лишь делители свободного члена в многочлене (если старший коэффициент многочлена равен единице, то все рациональные корни являются и целыми).
Схема Горнера (метод Горнера, правило Горнера) – алгоритм вычисления значения полинома (многочлена) при заданном значении неизвестной (переменной). Правило Горнера позволяет найти корни полинома, а также вычислить производные многочлена в заданной точке. Метод Горнера также является простым алгоритмом для деления многочлена на двучлен $$(x-a).$$
Пример:
Рассмотрим метод Горнера при делении многочлена $$P(x)=x^3-4x^2+2x+4$$ на двучлен $$x-2.$$
Решение:
Составим таблицу, состоящую из двух строк. В первую строку, начиная со второй ячейки, запишем коэффициенты полинома $$P(x)=x^3-4x^2+2x+4$$ по убыванию степеней неизвестной. В первую ячейку второй строки впишем $$a=2.$$
| $$1$$ | $$-4$$ | $$2$$ | $$4$$ | |
| $$2$$ |
Начнем заполнять пустые ячейки второй строки. Во вторую ячейку запишем 1 (просто переносим ее из второй ячейки первой строки). В третью ячейку запишем $$2\cdot1-4=-2$$ (во второй строке берем числа из первой и второй ячеек, находим их произведение и складываем его с числом из третьей ячейки первой строки), в четвертую записываем $$2\cdot(-2)+2=-2$$ (во второй строке берем числа из первой и третьей ячеек, находим их произведение и складываем его с числом из четвертой ячейки первой строки), аналогично в пятую записываем $$2\cdot(-2)+4=0.$$
| $$1$$ | $$-4$$ | $$2$$ | $$4$$ | |
| $$2$$ | $$1$$ | $$-2$$ | $$-2$$ | $$0$$ |
Числа второй строки (кроме первого и последнего) являются коэффициентами многочлена, полученного после деления многочлена $$P(x)=x^3-4x^2+2x+4$$ на двучлен $$x-2,$$ а последнее число второй строки – остатком от деления. В нашем случае получили: $$x^3-4x^2+2x+4=(x-2)(x^2-2x-2)+0$$ или $$x^3-4x^2+2x+4=(x-2)(x^2-2x-2)$$ – деление нацело.
Разложение многочленов на множители:
Если многочлен может быть разложен на множители (представлен в виде произведения двух или большего числа многочленов), то он называется приводимым (разложимым) на множители многочленов, иначе – неприводимым (неразложимым).
Основные способы разложения многочленов на множители:
- Вынесение общего множителя за скобки.
- Способ группировки.
- Применение формул сокращенного умножения.